lunes, agosto 27, 2007
viernes, junio 22, 2007
martes, mayo 29, 2007
CURISIDADES
Sabemos que un año no bisiesto tiene 365 días, pero sabías que:
102 +112 +122 = 365 = 132 +142
- Productos curiosos:
98765432 x 9 = 888.888.888
12345679 x 9 x 8 = 888.888.888
123456789 x 8 + 9 = 987654321
111.111.1112 = 12345678987654321
0 x 9 + 1 =
1
1 x 9 + 2 =
11
12 x 9 + 3 =
111
123 x 9 + 4 =
1111
1234 x 9 + 5 =
11111
12345 x 9 + 6 =
111111
123456 x 9 + 7 =
1111111
1234567 x 9 + 8 =
11111111
12345678 x 9 + 9 =
111111111
102 +112 +122 = 365 = 132 +142
- Productos curiosos:
98765432 x 9 = 888.888.888
12345679 x 9 x 8 = 888.888.888
123456789 x 8 + 9 = 987654321
111.111.1112 = 12345678987654321
0 x 9 + 1 =
1
1 x 9 + 2 =
11
12 x 9 + 3 =
111
123 x 9 + 4 =
1111
1234 x 9 + 5 =
11111
12345 x 9 + 6 =
111111
123456 x 9 + 7 =
1111111
1234567 x 9 + 8 =
11111111
12345678 x 9 + 9 =
111111111
lunes, mayo 21, 2007
domingo, mayo 20, 2007
687474703A2F2F7777772E6573746164697374696361736772617469732E636F6D2F65737461646973746963617320677261746973 |
| Estadisticas Gratis |
lunes, abril 30, 2007
Etimología de...
La palabra matemática viene del griego de mathema, cuyo significado era estudio de un tema.Lo que en la Edad Media se llamó Quadrivium, era las materias que antes Platón y Pitágoras enseñaron y eran: aritmética,astroomía, geometría y música.Y era lo que los griegos llamaban Mathematika.
JUEGO CON NÚMEROS........
Este es un pequeño jueguecillo que me pasaron el otro día en una presentación en Power Point. Consiste en llegar a 6, colocando símbolos matemáticos.
1 1 1 = 6
2 2 2 = 6
3 3 3 = 6
4 4 4 = 6
5 5 5 = 6
6 6 6 = 6
7 7 7 = 6
8 8 8 = 6
9 9 9 = 6
1 1 1 = 6
2 2 2 = 6
3 3 3 = 6
4 4 4 = 6
5 5 5 = 6
6 6 6 = 6
7 7 7 = 6
8 8 8 = 6
9 9 9 = 6
NÚMERO PI....
pi = 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46
jueves, marzo 29, 2007
miércoles, marzo 21, 2007
MATEMATICA DEL ROMANCE: a) . Hombre inteligente + mujer inteligente = romance b). Hombre inteligente + mujer tonta = aventura c). Hombre tonto + mujer inteligente = matrimonio d). Hombre tonto + mujer tonta = embarazo
ARITMETICA DE OFICINA: a). Jefe inteligente + empleado inteligente = beneficio b). Jefe inteligente + empleado tonto = producción c). Jefe tonto + empleado inteligente = ascenso d). Jefe tonto + empleado tonto = horas extras
MATEMATICA DE LAS COMPRAS: a.. Un hombre pagará 2,83 $; por un objeto de 1,83 $; que necesita. b.. Una mujer pagará 1,83 $; por un objeto de 2,83 $; que no necesita.
ECUACIONES Y ESTADISTICAS GENERALES: a). Una mujer se preocupa por el futuro hasta que encuentra marido. b). Un hombre nunca se preocupa por el futuro hasta que encuentra mujer. c). Un triunfador es un hombre que hace más dinero de lo que puede gastar su mujer d). Una triunfadora es la mujer que encuentra a ese hombre.
FELICIDAD: a). Para ser feliz con un hombre, tienes que entenderlo mucho y quererlo un poquito b). Para ser feliz con una mujer, tienes quequererla un montón y no intentar entenderla LONGEVIDAD: a). Los hombres casados viven más que los solteros, pero están mucho más dispuestos a morir
PROPENSION A LOS CAMBIOS: a). Una mujer se casa con un hombre esperando que cambie, pero no lo hace. b). Un hombre se casa con una mujer esperando que no cambie, pero sí lo hace.
TECNICAS DE DISCUSIÓN: a). Una mujer tiene siempre la última palabra en una discusión. b). Cualquier cosa que el hombre diga después de eso es el comienzo de una nueva discusión ...
ARITMETICA DE OFICINA: a). Jefe inteligente + empleado inteligente = beneficio b). Jefe inteligente + empleado tonto = producción c). Jefe tonto + empleado inteligente = ascenso d). Jefe tonto + empleado tonto = horas extras
MATEMATICA DE LAS COMPRAS: a.. Un hombre pagará 2,83 $; por un objeto de 1,83 $; que necesita. b.. Una mujer pagará 1,83 $; por un objeto de 2,83 $; que no necesita.
ECUACIONES Y ESTADISTICAS GENERALES: a). Una mujer se preocupa por el futuro hasta que encuentra marido. b). Un hombre nunca se preocupa por el futuro hasta que encuentra mujer. c). Un triunfador es un hombre que hace más dinero de lo que puede gastar su mujer d). Una triunfadora es la mujer que encuentra a ese hombre.
FELICIDAD: a). Para ser feliz con un hombre, tienes que entenderlo mucho y quererlo un poquito b). Para ser feliz con una mujer, tienes quequererla un montón y no intentar entenderla LONGEVIDAD: a). Los hombres casados viven más que los solteros, pero están mucho más dispuestos a morir
PROPENSION A LOS CAMBIOS: a). Una mujer se casa con un hombre esperando que cambie, pero no lo hace. b). Un hombre se casa con una mujer esperando que no cambie, pero sí lo hace.
TECNICAS DE DISCUSIÓN: a). Una mujer tiene siempre la última palabra en una discusión. b). Cualquier cosa que el hombre diga después de eso es el comienzo de una nueva discusión ...
Un equipo internacional resuelve un puzzle matemático de 248 dimensiones

Un equipo de científicos europeos y estadounidenses ha logrado elaborar el mapa de una de las estructuras más complicadas jamás estudiadas: el excepcional grupo de Lie E8. Esto podría tener implicaciones de enorme alcance en lo que se refiere a la comprensión del álgebra, la geometría, la teoría numérica, la gravedad cuántica y la química. Los grupos de Lie se ubican en la intersección entre dos campos fundamentales de las matemáticas: el álgebra y la geometría. Reciben su nombre del matemático noruego Sophus Lie, quien los estudió a finales del siglo XIX. En el proyecto Atlas, de cuatro años de duración, colaboran dieciocho matemáticos de Francia, Estados Unidos y Canadá. Según el Instituto Estadounidense de Matemáticas, «en su nivel más básico, el cálculo del E8 es una investigación de la simetría. Los matemáticos inventaron los grupos de Lie para captar la esencia de la simetría: en todo objeto simétrico, por ejemplo una esfera, se esconde un grupo de Lie.» Los grupos clásicos se describen como «colinas ondulantes poco pronunciadas que se extienden hacia el horizonte». También existen grupos más complejos, descritos como «picos muy pronunciados», y por encima de todos ellos destaca el E8, «un grupo de extraordinaria complejidad». El E8 representa las simetrías de un objeto de 57 dimensiones y tiene por sí mismo 248 dimensiones. Lo que este equipo ha logrado es describir cada uno de los elementos que forman el E8, así como las relaciones que los unen. La matriz tiene 205.263.363.600 entradas. Si se imprimieran con letra diminuta podrían cubrir una superficie equivalente a Manhattan. Si comparamos esta matriz con el mapa del genoma humano tenemos una idea clara del disparatado tamaño de la matriz. El genoma humano, que contiene toda la información genética de una célula, tiene un tamaño inferior a un gigabyte. El cálculo del E8 tiene un tamaño de 60 gigabytes. Como ocurre con el Proyecto Genoma Humano, no se sabrán las implicaciones que tendrá este mapa hasta dentro de muchos años. «Se trata de investigación fundamental que tendrá muchas repercusiones, la mayoría de las cuales aún no alcanzamos a comprender. Es como con el genoma humano, que no te proporciona al instante un medicamento nuevo y milagroso; nuestros resultados suponen un instrumento básico que se usará para avanzar la investigación en otros campos», señaló Jeffrey Adam, director del proyecto. Hermann Nicolai, director del Instituto Albert Einstein de Bonn (Alemania), explicó la importancia de este logro para la física. Los físicos se han topado con el E8 mucho más recientemente que los matemáticos, pero se les plantea con frecuencia cuando intentan unificar la gravedad con otras fuerzas fundamentales para formar una teoría coherente de la gravedad cuántica. «Así pues, comprender el funcionamiento interno del E8 no sólo supone un gran avance para las matemáticas puras, sino que además ayuda a los físicos en su búsqueda de una teoría unificada.»
Juegos Numéricos
1. Problemas Clásicos
Adivinando Números
Las propiedades y operaciones de los números a veces parecen casi mágicas.
Problema:
Explica por qué puedo adivinar los dos números que has pensado si me dices el resultado de estas operaciones:
Piensa un número.
Multiplícalo por dos.
Súmale 5.
Multiplica el resultado por 5.
Piensa otro número del 0 al 9.
Súmalo al resultado anterior.
Resta 25 al resultado obtenido.
Problema:
¿Cómo se puede justificar que sepa el resultado?
Escribe el año en que naciste
Súmale el año de algún acontecimiento importante de tu vida.
A este súmale los años que tendrás en 2007.
Finalmente, a eso súmale el número de años que van a transcurrir desde que se produjo el acontecimiento importante de tu vida hasta el año 2007.
La respuesta será 4014.
Problema:
Dile a alguien que piense un número de 3 cifras y que lo repita para formar un número de 6 cifras. Dile que se lo pase a alguien para que lo divida por 7. Observará que el resto de la división es 0. Dile a éste que le pase el resultado a otro para que lo divida por 11. Este a su vez le pasa el resultado a otro para que lo divida por 13 y que escriba el resultado en un papel. Si ahora abrimos el papel veremos que contiene el número pensado inicialmente. ¿Puedes explicarlo?
Problemas de velocidades.
Problema:
Dos muchachos que pasean en bicicleta, se hallan a 20 kilómetros uno del otro. En este momento empiezan a ir al uno hacia al otro, al mismo tiempo que una mosca que está posada en el manillar de una de las bicicletas empieza a volar hacia el otro. En el momento en que llega al manillar de la otra bicicleta da la vuelta y vuelve hacia la primera, y así sucesivamente. Si cada bicicleta se mueve a 10 kmts/h y la mosca a 15kmts/h, ¿qué distancia habrá volado la mosca cuando se encuentren las 2 bicicletas?
Problema:
Un pescador que llevaba un gran sombrero de paja estaba remando corriente arriba por un río cuya corriente llevaba una velocidad de 3 kmts/h. En cierto momento el sombrero se le cayó al agua, aunque no se dio cuenta hasta que estuvo a 5 kmts de distancia. En ese momento empezó a remar corriente abajo hasta que los recogió. En aguas quietas la velocidad con la que rema el pescador es de 5 kmts/h, por tanto su velocidad corriente arriba será de 2 kmts/h, mientras que corriente abajo será de 8 kmts/h. Si el pescador perdió su sombrero a las 2 de la tarde, ¿a que hora lo recuperó?
Problema:
El Sr. Martínez tiene que hacer un viaje de ida a vuelta a Teruel, y le gustaría llevar una velocidad promedio de 90 kmts/h entre la ida y la vuelta. Tras el viaje de ida, en el que ha hecho muchas paradas, calcula que su velocidad promedio en la ida a sido de 45 kmts/h. ¿A qué velocidad habrá de hacer la vuelta para cumplir su objetivo inicial?
Problema:
Un avión vuela de Madrid a Alicante, ida y vuelta. La velocidad del avión, cuando no hay viento, es de 800 kmts/h. Sin embargo, durante los dos trayectos ha habido un fuerte viento de 200 kmts/h en la dirección de Madrid a Alicante. ¿Como afectará ese viento a la duración total del viaje de ida y vuelta?
La respuesta al problema parecería ser que la velocidad del avión se ve aumentada por el viento a la ida en la misma medida en que es disminuida a la vuelta. Por tanto ambas influencias se compensan y el viaje durará igual que si no hubiera habido viento.Sin embargo, si consideramos el caso extremo de que la velocidad del viento fuera de 800 kmts/h el avión no podría regresar de Alicante y la duración del viaje de ida y vuelta sería infinita.
¿Cómo explicas la discrepancia entre los dos razonamientos?
Problema:
El Sr. Martínez llega todos los días a su estación de tren, después del trabajo, a las 5 en punto de la tarde. Allí le recoge su mujer y le lleva en coche a casa. Un día toma un tren anterior, llegando a su estación a las 4 en punto. En lugar de esperar hasta las 5 decide pasear hasta su casa. Por el camino le encuentra su mujer que le recoge con el coche, llegando a su casa 10 minutos antes de lo habitual. ¿Cuánto tiempo caminó el Sr.Martínez?
Problema:
Pepe y Pablo hacen footing desde A hasta B. Pepe corre la mitad de la distancia y anda la otra mitad. Pablo corre la mitad del tiempo y anda la otra mitad. Los dos corren a la misma velocidad y los dos andan a la misma velocidad. ¿Quién llega antes?
Problema:
Un señor llegó hasta un puente ferroviario y empezó a correr por él. Cuando había recorrido 3/8 del puente oyó el silbato del tren. Calculó inmediatamente: si retrocedo al comienzo llego exactamente en el momento en el que el tren entra en el puente, corriendo a mi velocidad de 10 Km/h y si corro hasta el final a esta velocidad llego allá al mismo tiempo que el tren. ¿A qué velocidad marcha ese tren?
Acertijos con dinero
Los problemas de esta sección están sacados del libro Matemática para divertirse de Martin Gardner publicado por Zugarto Ediciones en 1992 (Versión Original: Entertaining Mathematical Puzzles, Dover Publications, New York, 1986).
Problema:
"Déme cambio de 100 ptas", dijo el cliente."Lo siento", dijo el cajero, "con las monedas que tengo me es imposible"."¿Puede entonces darme cambio de 50 ptas?""Lo cierto es que no puedo darle cambio ni de 50, ni de 25, ni de 10, ni de 5 ptas.""¿Es que no tiene ninguna moneda?", preguntó el cliente.Tengo exactamente 125 ptas, contestó el cajero.
¿Qué monedas tiene el cajero?
La asignación de Pepito.
Pepito quería que su padre le diera 1000 ptas a la semana, pero su padre se negaba a darle más de 500. Ante la falta de acuerdo Pepito le propuso a su padre: "¿Por qué no ma das 1 pta hoy, 2 ptas la semana que viene, 4 la siguiente, y así sucesivamente?" "Por cuánto tiempo", preguntó si padre. "Solamente hasta mi cumpleaños, después ya negociaremos otra vez".Si quedan 30 semanas para el cumpleaños de pepito, ¿cuál de las siguientes cantidades crees que se acerca más al dinero que debería recibir Pepito?
1.000 ptas
10.000 ptas
100.000 ptas
Problema:
Supongamos que estás negociando el salario con tu Jefe y éste te da a elegir entre 2 ofertas:
2.000.000 por tu primer año de trabajo y un aumento de 400.000 ptas anuales en los 5 años siguientes.
1.000.000 por tu primer semestre de trabajo y un aumento de 100.000 ptas cada semestre durante los 5 años siguientes.
¿Qué oferta elegirías y por qué?
Problema (Reparto Justo):
Tres hombres en el desierto tienen 8 panes para comer, el primer hombre no tiene ningún pan, el segundo tiene tres panes y el tercero tiene cinco. Al llegar a un oasis el primer hombre quiere pagar a los otros dos la parte de los panes que él ha comido, toma ocho monedas y da tres monedas al segundo hombre y cinco al tercero.¿Es justo este reparto?
Problema:
Los hermanos Zipi y Zape me encargaron que vendiera en el mercado dos partidas de melones. Zipi me encargó 30 melones que debían ser vendidos al precio de 3 por una moneda de 500 pts; Zape me entregó también 30 melones para los que estipuló un precio más caro: 2 melones por una moneda de 500 pts. Lógicamente, después de efectuada la venta Zipi tendría que recibir 10 monedas de 500 pts y Zape 15. El total de la venta sería pues 25 monedas de 500 pts. Para mayor comodidad, empecé a venderlos en lotes de 5 por 1000 pts: Si tenía que vender 3 por 500 pts y luego 2 por 500 pts, sería más sencillo vender 5 por 1000 pts. Vendidos los 60 melones en 12 lotes de cinco melones cada uno, recibí 24 monedas de 500 pts.¿Cómo se explica esta diferencia de 500 pts entre lo recibido y lo que se supone que habría que recibir?
Curioso Testamento
Un rico abogado poseía 11 autos antiguos de gran valor. Cuando el abogado murió dejó un curioso testamento. En él pedía que sus 11 coches fueran repartidos entre sus tres hijos. La mitad de los autos debía ser para el hijo mayor; la cuarta parte para el mediano, y la sexta parte, para el benjamín.
Problema: ¿Cómo realizarías este reparto?
Mientras los hijos piensan cómo hacer el reparto se acercó en su deportivo nuevo una famosa especialista en numerología. Cuando los chicos le contaron su situación, la señora, muy generosa, aparcó su deportivo junto a los otros coches y procedió al reparto dando la mitad del total, o sea, seis, al hijo mayor. El mediano se llevó la cuarta parte de 12, es decir, tres. Y el menor, la sexta parte de 12, o sea dos.Al terminar el reparto la señora se cercioró de que 6+3+2 = 11. Así que sobra un coche ¡el de ella! ¡Me alegro de haberos sido útil!, les dijo, ¡ya os enviaré la minuta!
Problema: ¿Cómo ha sido posible dicho reparto?
Problema: Supongamos ahora que la herencia constaba de 35 coches que debían repartirse del siguiente modo: ½ para el mayor 1/3 para el mediano y 1/9 para el pequeño. Además, la especialista en numerología quiere como honorarios uno de los coches. ¿Cómo se solucionaría el problema? Comprueba qué pasaría con las cantidades 53, 71 y este mismo reparto (1/2, 1/3, 1/9).
Problema: Se dispone de un saco con 8 monedas de oro, no todas del mismo valor: hay una que vale 300.000 pts., y las demás tiene un valor de 100.000 pts., 500.000 pts. ó de 1.000.000 pts. Cierto testamento indica que dichas monedas deben ser repartidas, sin ser vendidas, entre cuatro hermanos dando: 1/3 del valor total al hermano mayor, 1/4 al segundo, 1/5 al tercero y 1/6 para el pequeño. Ante el problema de semejante reparto, el abogado que llevaba el caso les propuso lo siguiente: él tenía una moneda de oro por valor de 100.000 pts, que añadió al saco de las 8 monedas y convino que daría a cada uno su parte siempre y cuando él pudiera quedarse con el saco. Los hermanos se aceptaron agradecidos, pues cada uno recibía así monedas por más valor de lo que le correspondía. Al salir del bufete se percataron de que entre todos habían recibido 8 monedas de oro pero ninguno tenía la moneda que valía 300.000 pts. ¿Cuál era el valor total de las 8 monedas? ¿Qué monedas recibió cada uno de los hermanos?.
Problema (Otro testamento):
Un rajá dejó a sus hijas cierto número de perlas y determinó que la división se hiciera del siguiente modo: La hija mayor se quedaría con una perla y 1/7 de lo que quedara. La segunda hija recibiría dos perlas y 1/7 de lo restante, la tercera joven recibiría 3 perlas y 1/7 de lo que quedara. Y así sucesivamente. Hecha la división cada una de las hijas recibió el mismo número de perlas.¿Cuántas perlas había? ¿Cuántas eran las hijas del rajá ?
Los Cuatro Cuatros
El problema de los cuatro cuatros es el siguiente: Escribir con cuatro cuatros y signos matemáticos una expresión que sea igual a un número entero dado. En la expresión no puede figurar, aparte de los cuatro cuatros, ninguna cifra o letra o símbolo algebraico que suponga letras, tal como: log, lim, etc. Pero si puede usarse la parte entera.Afirman los pacientes calculadores que será posible escribir con cuatro cuatros todos los números enteros desde 0 hasta 100. A veces será necesario recurrir al signo de factorial ( ! ) y al de la raíz cuadrada. La raíz cúbica no puede ser empleada a causa del índice 3.
Problema: Escribe con cuatro cuatros todos los números del 0 al 100.
Problemas con vasijas
Problema:
Un hombre va a una fuente a buscar exactamente 4 litros de agua pero sólo dispone de dos recipientes: un cubo de 5 litros de capacidad y una botella de 3 litros. ¿Cómo puede obtener en estas condiciones exactamente 4 litros?
Problema: Ahora se dispone de un suministro ilimitado de agua, un gran cubo con un desagüe y de dos vasijas que, una vez llenas, contienen exactamente 7 y 9 litros de agua. ¿Cómo se puede, con estos recursos, medir exactamente un litro de agua?
Problema: Tenemos dos vasijas, una vasija A con 10 litros de vino y una vasija B con 10 litros de agua. Tomamos un litro de agua de la vasija A y lo echamos en la vasija B. Tomamos un litro de la mezcla de la vasija B y lo echamos en la vasija A. De la mezcla existente en la vasija A tomamos un litro y lo echamos de nuevo en la vasija B. Continuamos este proceso. Al final de 10 trasvases, ¿habrá más agua en la vasija B que vino en la A, o viceversa? ¿Y si repetimos el proceso infinitas veces?
¿Cómo escapar de una torre?
Este acertijo ha sido extraído del libro The Moscow Puzzles, de Boris A. Kordemsky.Hace 300 años vivió un príncipe de corazón enfermo y excesivo orgullo. Éste había prometido a su hija en matrimonio a un rico vecino, pero ésta tenía un plan diferente. Enamorada de un lacayo, intentó huir con él a las montañas, pero fueron capturados.El príncipe decidió ejecutarlos al día siguiente. Los encerró en una alta torre junto con una muchacha, una sirviente que los había ayudado en su fallida huida. Mirando por la ventana, observaron que era imposible saltar y sobrevivir. Sin embargo, había una cuerda, colgando de una polea, en cuyos extremos había sendas cestas. Éstas habían sido utilizadas en el pasado para subir ladrillos y bajar escombros. También había en la torre 13 trozos de cadena de unos 5 kilogramos cada uno.Los prisioneros dedujeron que si una de las cestas llevaba una carga superior en cinco kilogramos a la otra, la más pesada descendería suavemente al suelo a la vez que la otra ascendía hacia la ventana.
Problema: Sabiendo que los pesos de los prisioneros eran, respectivamente, de 90, 50 y 40 kilogramos, ¿cómo podrían escapar de la torre? En ningún momento una cesta en descenso puede pesar 5 kilogramos más que la otra. ¿Cuántas veces han bajado las cestas?
Sobre relojes
Problema: Susana y Miguel conciertan una cita a las ocho de la tarde. El reloj de Susana está atrasado 10 minutos, pero ella cree que está 5 minutos adelantado. El reloj de Miguel está adelantado 5 minutos, pero él cree que está atrasado 10. ¿Quién llegará antes a la cita?
Problema:
Tenemos tres cajas idénticas. Una contiene relojes deportivos; la otra, relojes de oro, y la tercera, mezcla de relojes deportivos y de oro.
Están etiquetadas con las referencias DD, OO y DO, pero ninguna
caja lleva la etiqueta que le corresponde. El dependiente dice
que si me da una caja y yo saco un reloj y se lo enseño, puede
adivinar el contenido de todas las cajas. Si crees que es
cierto lo que dice el dependiente, explica cómo lo
consigue.
El Problema de Josephus
Josephus Flavius fue un famoso historiador judío de la primera centuria (37-100). Cuentan que durante la guerra de los judíos y los romanos, él se quedó atrapado, con otros cuarenta soldados judíos, en una cueva asediada por los romanos y sin una posible vía de escape.La leyenda dice que, prefiriendo suicidarse a ser capturados, los soldados decidieron matarse entre ellos, pero Josephus y un amigo suyo no estaban de acuerdo. Para sobrevivir Josephus sugirió que se procediera del siguiente modo:Todos ellos debían colocarse en círculo, numerándose del 1 al 41, y empezando a contar por el primero toda tercera persona sería asesinada hasta que sólo quedara una persona que debería suicidarse. Josephus salvó su vida y la de su amigo colocándose en el lugar 31 y 16 respectivamente.
Problema:
Comprueba que las dos últimas personas que quedaron fueron Josephus y su amigo.
Adivinando Números
Las propiedades y operaciones de los números a veces parecen casi mágicas.
Problema:
Explica por qué puedo adivinar los dos números que has pensado si me dices el resultado de estas operaciones:
Piensa un número.
Multiplícalo por dos.
Súmale 5.
Multiplica el resultado por 5.
Piensa otro número del 0 al 9.
Súmalo al resultado anterior.
Resta 25 al resultado obtenido.
Problema:
¿Cómo se puede justificar que sepa el resultado?
Escribe el año en que naciste
Súmale el año de algún acontecimiento importante de tu vida.
A este súmale los años que tendrás en 2007.
Finalmente, a eso súmale el número de años que van a transcurrir desde que se produjo el acontecimiento importante de tu vida hasta el año 2007.
La respuesta será 4014.
Problema:
Dile a alguien que piense un número de 3 cifras y que lo repita para formar un número de 6 cifras. Dile que se lo pase a alguien para que lo divida por 7. Observará que el resto de la división es 0. Dile a éste que le pase el resultado a otro para que lo divida por 11. Este a su vez le pasa el resultado a otro para que lo divida por 13 y que escriba el resultado en un papel. Si ahora abrimos el papel veremos que contiene el número pensado inicialmente. ¿Puedes explicarlo?
Problemas de velocidades.
Problema:
Dos muchachos que pasean en bicicleta, se hallan a 20 kilómetros uno del otro. En este momento empiezan a ir al uno hacia al otro, al mismo tiempo que una mosca que está posada en el manillar de una de las bicicletas empieza a volar hacia el otro. En el momento en que llega al manillar de la otra bicicleta da la vuelta y vuelve hacia la primera, y así sucesivamente. Si cada bicicleta se mueve a 10 kmts/h y la mosca a 15kmts/h, ¿qué distancia habrá volado la mosca cuando se encuentren las 2 bicicletas?
Problema:
Un pescador que llevaba un gran sombrero de paja estaba remando corriente arriba por un río cuya corriente llevaba una velocidad de 3 kmts/h. En cierto momento el sombrero se le cayó al agua, aunque no se dio cuenta hasta que estuvo a 5 kmts de distancia. En ese momento empezó a remar corriente abajo hasta que los recogió. En aguas quietas la velocidad con la que rema el pescador es de 5 kmts/h, por tanto su velocidad corriente arriba será de 2 kmts/h, mientras que corriente abajo será de 8 kmts/h. Si el pescador perdió su sombrero a las 2 de la tarde, ¿a que hora lo recuperó?
Problema:
El Sr. Martínez tiene que hacer un viaje de ida a vuelta a Teruel, y le gustaría llevar una velocidad promedio de 90 kmts/h entre la ida y la vuelta. Tras el viaje de ida, en el que ha hecho muchas paradas, calcula que su velocidad promedio en la ida a sido de 45 kmts/h. ¿A qué velocidad habrá de hacer la vuelta para cumplir su objetivo inicial?
Problema:
Un avión vuela de Madrid a Alicante, ida y vuelta. La velocidad del avión, cuando no hay viento, es de 800 kmts/h. Sin embargo, durante los dos trayectos ha habido un fuerte viento de 200 kmts/h en la dirección de Madrid a Alicante. ¿Como afectará ese viento a la duración total del viaje de ida y vuelta?
La respuesta al problema parecería ser que la velocidad del avión se ve aumentada por el viento a la ida en la misma medida en que es disminuida a la vuelta. Por tanto ambas influencias se compensan y el viaje durará igual que si no hubiera habido viento.Sin embargo, si consideramos el caso extremo de que la velocidad del viento fuera de 800 kmts/h el avión no podría regresar de Alicante y la duración del viaje de ida y vuelta sería infinita.
¿Cómo explicas la discrepancia entre los dos razonamientos?
Problema:
El Sr. Martínez llega todos los días a su estación de tren, después del trabajo, a las 5 en punto de la tarde. Allí le recoge su mujer y le lleva en coche a casa. Un día toma un tren anterior, llegando a su estación a las 4 en punto. En lugar de esperar hasta las 5 decide pasear hasta su casa. Por el camino le encuentra su mujer que le recoge con el coche, llegando a su casa 10 minutos antes de lo habitual. ¿Cuánto tiempo caminó el Sr.Martínez?
Problema:
Pepe y Pablo hacen footing desde A hasta B. Pepe corre la mitad de la distancia y anda la otra mitad. Pablo corre la mitad del tiempo y anda la otra mitad. Los dos corren a la misma velocidad y los dos andan a la misma velocidad. ¿Quién llega antes?
Problema:
Un señor llegó hasta un puente ferroviario y empezó a correr por él. Cuando había recorrido 3/8 del puente oyó el silbato del tren. Calculó inmediatamente: si retrocedo al comienzo llego exactamente en el momento en el que el tren entra en el puente, corriendo a mi velocidad de 10 Km/h y si corro hasta el final a esta velocidad llego allá al mismo tiempo que el tren. ¿A qué velocidad marcha ese tren?
Acertijos con dinero
Los problemas de esta sección están sacados del libro Matemática para divertirse de Martin Gardner publicado por Zugarto Ediciones en 1992 (Versión Original: Entertaining Mathematical Puzzles, Dover Publications, New York, 1986).
Problema:
"Déme cambio de 100 ptas", dijo el cliente."Lo siento", dijo el cajero, "con las monedas que tengo me es imposible"."¿Puede entonces darme cambio de 50 ptas?""Lo cierto es que no puedo darle cambio ni de 50, ni de 25, ni de 10, ni de 5 ptas.""¿Es que no tiene ninguna moneda?", preguntó el cliente.Tengo exactamente 125 ptas, contestó el cajero.
¿Qué monedas tiene el cajero?
La asignación de Pepito.
Pepito quería que su padre le diera 1000 ptas a la semana, pero su padre se negaba a darle más de 500. Ante la falta de acuerdo Pepito le propuso a su padre: "¿Por qué no ma das 1 pta hoy, 2 ptas la semana que viene, 4 la siguiente, y así sucesivamente?" "Por cuánto tiempo", preguntó si padre. "Solamente hasta mi cumpleaños, después ya negociaremos otra vez".Si quedan 30 semanas para el cumpleaños de pepito, ¿cuál de las siguientes cantidades crees que se acerca más al dinero que debería recibir Pepito?
1.000 ptas
10.000 ptas
100.000 ptas
Problema:
Supongamos que estás negociando el salario con tu Jefe y éste te da a elegir entre 2 ofertas:
2.000.000 por tu primer año de trabajo y un aumento de 400.000 ptas anuales en los 5 años siguientes.
1.000.000 por tu primer semestre de trabajo y un aumento de 100.000 ptas cada semestre durante los 5 años siguientes.
¿Qué oferta elegirías y por qué?
Problema (Reparto Justo):
Tres hombres en el desierto tienen 8 panes para comer, el primer hombre no tiene ningún pan, el segundo tiene tres panes y el tercero tiene cinco. Al llegar a un oasis el primer hombre quiere pagar a los otros dos la parte de los panes que él ha comido, toma ocho monedas y da tres monedas al segundo hombre y cinco al tercero.¿Es justo este reparto?
Problema:
Los hermanos Zipi y Zape me encargaron que vendiera en el mercado dos partidas de melones. Zipi me encargó 30 melones que debían ser vendidos al precio de 3 por una moneda de 500 pts; Zape me entregó también 30 melones para los que estipuló un precio más caro: 2 melones por una moneda de 500 pts. Lógicamente, después de efectuada la venta Zipi tendría que recibir 10 monedas de 500 pts y Zape 15. El total de la venta sería pues 25 monedas de 500 pts. Para mayor comodidad, empecé a venderlos en lotes de 5 por 1000 pts: Si tenía que vender 3 por 500 pts y luego 2 por 500 pts, sería más sencillo vender 5 por 1000 pts. Vendidos los 60 melones en 12 lotes de cinco melones cada uno, recibí 24 monedas de 500 pts.¿Cómo se explica esta diferencia de 500 pts entre lo recibido y lo que se supone que habría que recibir?
Curioso Testamento
Un rico abogado poseía 11 autos antiguos de gran valor. Cuando el abogado murió dejó un curioso testamento. En él pedía que sus 11 coches fueran repartidos entre sus tres hijos. La mitad de los autos debía ser para el hijo mayor; la cuarta parte para el mediano, y la sexta parte, para el benjamín.
Problema: ¿Cómo realizarías este reparto?
Mientras los hijos piensan cómo hacer el reparto se acercó en su deportivo nuevo una famosa especialista en numerología. Cuando los chicos le contaron su situación, la señora, muy generosa, aparcó su deportivo junto a los otros coches y procedió al reparto dando la mitad del total, o sea, seis, al hijo mayor. El mediano se llevó la cuarta parte de 12, es decir, tres. Y el menor, la sexta parte de 12, o sea dos.Al terminar el reparto la señora se cercioró de que 6+3+2 = 11. Así que sobra un coche ¡el de ella! ¡Me alegro de haberos sido útil!, les dijo, ¡ya os enviaré la minuta!
Problema: ¿Cómo ha sido posible dicho reparto?
Problema: Supongamos ahora que la herencia constaba de 35 coches que debían repartirse del siguiente modo: ½ para el mayor 1/3 para el mediano y 1/9 para el pequeño. Además, la especialista en numerología quiere como honorarios uno de los coches. ¿Cómo se solucionaría el problema? Comprueba qué pasaría con las cantidades 53, 71 y este mismo reparto (1/2, 1/3, 1/9).
Problema: Se dispone de un saco con 8 monedas de oro, no todas del mismo valor: hay una que vale 300.000 pts., y las demás tiene un valor de 100.000 pts., 500.000 pts. ó de 1.000.000 pts. Cierto testamento indica que dichas monedas deben ser repartidas, sin ser vendidas, entre cuatro hermanos dando: 1/3 del valor total al hermano mayor, 1/4 al segundo, 1/5 al tercero y 1/6 para el pequeño. Ante el problema de semejante reparto, el abogado que llevaba el caso les propuso lo siguiente: él tenía una moneda de oro por valor de 100.000 pts, que añadió al saco de las 8 monedas y convino que daría a cada uno su parte siempre y cuando él pudiera quedarse con el saco. Los hermanos se aceptaron agradecidos, pues cada uno recibía así monedas por más valor de lo que le correspondía. Al salir del bufete se percataron de que entre todos habían recibido 8 monedas de oro pero ninguno tenía la moneda que valía 300.000 pts. ¿Cuál era el valor total de las 8 monedas? ¿Qué monedas recibió cada uno de los hermanos?.
Problema (Otro testamento):
Un rajá dejó a sus hijas cierto número de perlas y determinó que la división se hiciera del siguiente modo: La hija mayor se quedaría con una perla y 1/7 de lo que quedara. La segunda hija recibiría dos perlas y 1/7 de lo restante, la tercera joven recibiría 3 perlas y 1/7 de lo que quedara. Y así sucesivamente. Hecha la división cada una de las hijas recibió el mismo número de perlas.¿Cuántas perlas había? ¿Cuántas eran las hijas del rajá ?
Los Cuatro Cuatros
El problema de los cuatro cuatros es el siguiente: Escribir con cuatro cuatros y signos matemáticos una expresión que sea igual a un número entero dado. En la expresión no puede figurar, aparte de los cuatro cuatros, ninguna cifra o letra o símbolo algebraico que suponga letras, tal como: log, lim, etc. Pero si puede usarse la parte entera.Afirman los pacientes calculadores que será posible escribir con cuatro cuatros todos los números enteros desde 0 hasta 100. A veces será necesario recurrir al signo de factorial ( ! ) y al de la raíz cuadrada. La raíz cúbica no puede ser empleada a causa del índice 3.
Problema: Escribe con cuatro cuatros todos los números del 0 al 100.
Problemas con vasijas
Problema:
Un hombre va a una fuente a buscar exactamente 4 litros de agua pero sólo dispone de dos recipientes: un cubo de 5 litros de capacidad y una botella de 3 litros. ¿Cómo puede obtener en estas condiciones exactamente 4 litros?
Problema: Ahora se dispone de un suministro ilimitado de agua, un gran cubo con un desagüe y de dos vasijas que, una vez llenas, contienen exactamente 7 y 9 litros de agua. ¿Cómo se puede, con estos recursos, medir exactamente un litro de agua?
Problema: Tenemos dos vasijas, una vasija A con 10 litros de vino y una vasija B con 10 litros de agua. Tomamos un litro de agua de la vasija A y lo echamos en la vasija B. Tomamos un litro de la mezcla de la vasija B y lo echamos en la vasija A. De la mezcla existente en la vasija A tomamos un litro y lo echamos de nuevo en la vasija B. Continuamos este proceso. Al final de 10 trasvases, ¿habrá más agua en la vasija B que vino en la A, o viceversa? ¿Y si repetimos el proceso infinitas veces?
¿Cómo escapar de una torre?
Este acertijo ha sido extraído del libro The Moscow Puzzles, de Boris A. Kordemsky.Hace 300 años vivió un príncipe de corazón enfermo y excesivo orgullo. Éste había prometido a su hija en matrimonio a un rico vecino, pero ésta tenía un plan diferente. Enamorada de un lacayo, intentó huir con él a las montañas, pero fueron capturados.El príncipe decidió ejecutarlos al día siguiente. Los encerró en una alta torre junto con una muchacha, una sirviente que los había ayudado en su fallida huida. Mirando por la ventana, observaron que era imposible saltar y sobrevivir. Sin embargo, había una cuerda, colgando de una polea, en cuyos extremos había sendas cestas. Éstas habían sido utilizadas en el pasado para subir ladrillos y bajar escombros. También había en la torre 13 trozos de cadena de unos 5 kilogramos cada uno.Los prisioneros dedujeron que si una de las cestas llevaba una carga superior en cinco kilogramos a la otra, la más pesada descendería suavemente al suelo a la vez que la otra ascendía hacia la ventana.
Problema: Sabiendo que los pesos de los prisioneros eran, respectivamente, de 90, 50 y 40 kilogramos, ¿cómo podrían escapar de la torre? En ningún momento una cesta en descenso puede pesar 5 kilogramos más que la otra. ¿Cuántas veces han bajado las cestas?
Sobre relojes
Problema: Susana y Miguel conciertan una cita a las ocho de la tarde. El reloj de Susana está atrasado 10 minutos, pero ella cree que está 5 minutos adelantado. El reloj de Miguel está adelantado 5 minutos, pero él cree que está atrasado 10. ¿Quién llegará antes a la cita?
Problema:
Tenemos tres cajas idénticas. Una contiene relojes deportivos; la otra, relojes de oro, y la tercera, mezcla de relojes deportivos y de oro.
Están etiquetadas con las referencias DD, OO y DO, pero ninguna
caja lleva la etiqueta que le corresponde. El dependiente dice
que si me da una caja y yo saco un reloj y se lo enseño, puede
adivinar el contenido de todas las cajas. Si crees que es
cierto lo que dice el dependiente, explica cómo lo
consigue.
El Problema de Josephus
Josephus Flavius fue un famoso historiador judío de la primera centuria (37-100). Cuentan que durante la guerra de los judíos y los romanos, él se quedó atrapado, con otros cuarenta soldados judíos, en una cueva asediada por los romanos y sin una posible vía de escape.La leyenda dice que, prefiriendo suicidarse a ser capturados, los soldados decidieron matarse entre ellos, pero Josephus y un amigo suyo no estaban de acuerdo. Para sobrevivir Josephus sugirió que se procediera del siguiente modo:Todos ellos debían colocarse en círculo, numerándose del 1 al 41, y empezando a contar por el primero toda tercera persona sería asesinada hasta que sólo quedara una persona que debería suicidarse. Josephus salvó su vida y la de su amigo colocándose en el lugar 31 y 16 respectivamente.
Problema:
Comprueba que las dos últimas personas que quedaron fueron Josephus y su amigo.
lunes, febrero 26, 2007
"Romance de la derivada y el arcotangente"
Veraneaba una derivada enésima en un pequeño chalet situado en larecta del infinito del plano de Gauss, cuando conoció a un arcotangentesimpatiquísimo y de espléndida representación gráfica, que ademáspertenecía a una de las mejores familias trigonométricas. Enseguida notaron que tenían propiedades comunes. Un día, en casa deuna parábola que había ido a pasar allí una temporada con sus ramasalejadas, se encontraron en un punto aislado de ambiente muy íntimo.Se dieron cuenta que convergían hacia límites cuya diferencia era tanpequeña como se quisiera. Había nacido un romance. Acaramelados en un entorno de radio épsilon,se dijeron mil teoremas de amor. Cuando el verano pasó, y las parábolashabían vuelto al origen, la derivada y el arcotangente eran novios.Entonces, empezaron los largos paseos por las asíntotas siempre unidospor un punto común, los interminables desarrollos en serie bajo losconoides llorosos del lago, las innumerables sesiones de proyecciónortogonal. Hasta fueron al circo, donde vieron a un tropel de funcioneslogarítmicas dar saltos infinitos en sus discontinuidades. En fin, lo que eternamente hacían los novios. Entonces, empezaron los largos paseos por las asíntotas siempreunidos por un punto común, los interminables desarrollos en serie bajolos conoides llorosos del lago, las innumerables sesiones de proyecciónortogonal. Hasta fueron al circo, donde vieron a un tropel de funcioneslogarítmicas dar saltos infinitos en sus discontinuidades. En fin, loque eternamente hacían los novios. Durante un baile organizado por unas cartesianas, primas delarcotangente, la pareja pudo tener el mismo radio de curvatura envarios puntos. Las series melódicas eran de ritmos uniformementecrecientes y la pareja giraba entrelazada alrededor de un mismo puntodoble. Del amor había nacido la pasión. Enamorados locamente, susgráficas coincidían en más y más puntos. Con el beneficio de las ventasde unas fincas que tenía en el campo complejo, el arcotangente compróun recinto cerrado en el plano de Riemann. En la decoración se gastó hasta el último infinitésimo. Adornó lasparedes con unas tablas de potenciales de "e" preciosas, puso varioscuartos de divisiones del término independiente que costaron una burrada.Empapeló las habitaciones con las gráficas de las funciones másconocidas, y puso varios paraboloides de revolución chinos de los quesurgían desarrollables tangenciales en flor. Y Bernouilli le prestó sulemniscata para adornar su salón durante los primeros días. Cuando todo estuvo preparado, el arcotangente se trasladó al puntoimpropio y contempló satisfecho su dominio de existencia. Varios díasdespués fué en busca de la derivada de orden n y cuando llevaban unrato charlando de variables arbitrarias, le espetó, sin más: ¿Por quéno vamos a tomar unos neperianos a mi apartamento? De paso lo conocerías,ha quedado monísimo. A ella, que le quedaba muy poco para anularse,tras una breve discusión del resultado, aceptó. El novio le enseñó sudominio y quedó integrada. Los neperianos y una música armónica simplehicieron que entre sus puntos existiera una correspondencia unívoca.Unidos así, miraron a espacio euclideo. Los asteroides rutilaban en labóveda de Viviany... ¡Eran felices!- "¿No sientes calor?" Dijo ella.- "Yo sí, ¿y tú?".- "Yo también.".- "Ponte en forma canónica. Estarás más cómoda.". Entonces él le fue quitando constantes. Después de artificiosasoperaciones la puso en paramétricas racionales...- "¿Qué haces? Me da vergüenza...." dijo ella.- "Te amo, ¡yo estoy inverso por ti....!".- "Déjame besarte la ordenada en el origen....¡No seas cruel!.....¡ven!.".- "Dividamos por un momento la nomenclatura ordinaria y tendamos juntosal infinito.". Él le acarició sus máximos y sus mínimos y ella se sintió descomponeren fracciones simples. (Las siguientes operaciones quedan a la penetracióndel lector). Al cabo de algún tiempo, la derivada enésima perdió su periodicidad.Posteriores análisis algebraicos demostraron que su variable habíaquedado incrementada y su matriz era distinta de cero. Ella le confesóa él, saliéndole los colores "voy a ser primitiva de otra función". Élla respondió: "podríamos eliminar el parámetro elevando al cuadrado yrestando". "Eso es que ya no me quieres". "No seas irracional, claroque te quiero. Nuestras ecuaciones formarán una superficie cerrada,confía en mi". La boda se preparó en un tiempo diferencial de "t",para no dar que hablar en el círculo de los 9 puntos. Los padrinosfueron el padre de la novia, un polinomio lineal de exponente entero,y la madre del novio, una asiroide de noble asíntota. La novia lucíacoordenadas cilíndricas de "Satung" y velo de puntos imaginarios.Ofició la ceremonia Cayley, auxiliado por Pascal y el nuncioS.S.= Monseñor Ricatti. Hoy día el arcotangente tiene un buen puestoen una fábrica de series de Fourier, y ella cuida en casa de 5 lindostérminos de menor grado, producto cartesiano de su amor.
Veraneaba una derivada enésima en un pequeño chalet situado en larecta del infinito del plano de Gauss, cuando conoció a un arcotangentesimpatiquísimo y de espléndida representación gráfica, que ademáspertenecía a una de las mejores familias trigonométricas. Enseguida notaron que tenían propiedades comunes. Un día, en casa deuna parábola que había ido a pasar allí una temporada con sus ramasalejadas, se encontraron en un punto aislado de ambiente muy íntimo.Se dieron cuenta que convergían hacia límites cuya diferencia era tanpequeña como se quisiera. Había nacido un romance. Acaramelados en un entorno de radio épsilon,se dijeron mil teoremas de amor. Cuando el verano pasó, y las parábolashabían vuelto al origen, la derivada y el arcotangente eran novios.Entonces, empezaron los largos paseos por las asíntotas siempre unidospor un punto común, los interminables desarrollos en serie bajo losconoides llorosos del lago, las innumerables sesiones de proyecciónortogonal. Hasta fueron al circo, donde vieron a un tropel de funcioneslogarítmicas dar saltos infinitos en sus discontinuidades. En fin, lo que eternamente hacían los novios. Entonces, empezaron los largos paseos por las asíntotas siempreunidos por un punto común, los interminables desarrollos en serie bajolos conoides llorosos del lago, las innumerables sesiones de proyecciónortogonal. Hasta fueron al circo, donde vieron a un tropel de funcioneslogarítmicas dar saltos infinitos en sus discontinuidades. En fin, loque eternamente hacían los novios. Durante un baile organizado por unas cartesianas, primas delarcotangente, la pareja pudo tener el mismo radio de curvatura envarios puntos. Las series melódicas eran de ritmos uniformementecrecientes y la pareja giraba entrelazada alrededor de un mismo puntodoble. Del amor había nacido la pasión. Enamorados locamente, susgráficas coincidían en más y más puntos. Con el beneficio de las ventasde unas fincas que tenía en el campo complejo, el arcotangente compróun recinto cerrado en el plano de Riemann. En la decoración se gastó hasta el último infinitésimo. Adornó lasparedes con unas tablas de potenciales de "e" preciosas, puso varioscuartos de divisiones del término independiente que costaron una burrada.Empapeló las habitaciones con las gráficas de las funciones másconocidas, y puso varios paraboloides de revolución chinos de los quesurgían desarrollables tangenciales en flor. Y Bernouilli le prestó sulemniscata para adornar su salón durante los primeros días. Cuando todo estuvo preparado, el arcotangente se trasladó al puntoimpropio y contempló satisfecho su dominio de existencia. Varios díasdespués fué en busca de la derivada de orden n y cuando llevaban unrato charlando de variables arbitrarias, le espetó, sin más: ¿Por quéno vamos a tomar unos neperianos a mi apartamento? De paso lo conocerías,ha quedado monísimo. A ella, que le quedaba muy poco para anularse,tras una breve discusión del resultado, aceptó. El novio le enseñó sudominio y quedó integrada. Los neperianos y una música armónica simplehicieron que entre sus puntos existiera una correspondencia unívoca.Unidos así, miraron a espacio euclideo. Los asteroides rutilaban en labóveda de Viviany... ¡Eran felices!- "¿No sientes calor?" Dijo ella.- "Yo sí, ¿y tú?".- "Yo también.".- "Ponte en forma canónica. Estarás más cómoda.". Entonces él le fue quitando constantes. Después de artificiosasoperaciones la puso en paramétricas racionales...- "¿Qué haces? Me da vergüenza...." dijo ella.- "Te amo, ¡yo estoy inverso por ti....!".- "Déjame besarte la ordenada en el origen....¡No seas cruel!.....¡ven!.".- "Dividamos por un momento la nomenclatura ordinaria y tendamos juntosal infinito.". Él le acarició sus máximos y sus mínimos y ella se sintió descomponeren fracciones simples. (Las siguientes operaciones quedan a la penetracióndel lector). Al cabo de algún tiempo, la derivada enésima perdió su periodicidad.Posteriores análisis algebraicos demostraron que su variable habíaquedado incrementada y su matriz era distinta de cero. Ella le confesóa él, saliéndole los colores "voy a ser primitiva de otra función". Élla respondió: "podríamos eliminar el parámetro elevando al cuadrado yrestando". "Eso es que ya no me quieres". "No seas irracional, claroque te quiero. Nuestras ecuaciones formarán una superficie cerrada,confía en mi". La boda se preparó en un tiempo diferencial de "t",para no dar que hablar en el círculo de los 9 puntos. Los padrinosfueron el padre de la novia, un polinomio lineal de exponente entero,y la madre del novio, una asiroide de noble asíntota. La novia lucíacoordenadas cilíndricas de "Satung" y velo de puntos imaginarios.Ofició la ceremonia Cayley, auxiliado por Pascal y el nuncioS.S.= Monseñor Ricatti. Hoy día el arcotangente tiene un buen puestoen una fábrica de series de Fourier, y ella cuida en casa de 5 lindostérminos de menor grado, producto cartesiano de su amor.
sábado, febrero 24, 2007
martes, febrero 06, 2007
lunes, febrero 05, 2007
viernes, febrero 02, 2007
miércoles, enero 24, 2007
CÁLCULO DEL MÍNIMO COMÚN MÚLTIPLO DE UNOS NÚMEROS
Vamos a obtener el m.c.m., o sea el menor múltiplo común, de tres números: 5, 10 y 4
Para ello debemos descomponer en factores los tres números:
4 = 22
10 = 2 . 5
5 = 5
Ahora tomamos todos los factores comunes y no comunes con el mayor exponente y los multiplicamos
m.c.m. = 5 . 22 = 5 . 4 = 20
Para ello debemos descomponer en factores los tres números:
4 = 22
10 = 2 . 5
5 = 5
Ahora tomamos todos los factores comunes y no comunes con el mayor exponente y los multiplicamos
m.c.m. = 5 . 22 = 5 . 4 = 20
Mínimo Común Múltiplo (m.c.m.)
El mínimo común múltiplo (m. c. m.) de dos o más números es el menor múltiplo común distinto de cero.
Ejemplo: Averiguar el m.c.m. de Sacar el M.C.D. de 20 y 10:
20:
20, 40, 60, 80...
10:
10, 20, 30...
20 es el múltiplo menor que es común a ambos números.
Multiplos: los múltiplos de un número se obtienen multiplicando dicho número por los números naturales 0, 1, 2, 3, 4, 5.....
Ejemplo: múltiplos del 7: 7x0=0; 7x1=7; 7x2=14; 7x3=21; 7x4=28; 7x5=35 ....
O sea son múltiplos del 7:, 0, 7, 14, 21, 28, 35, 42, 48, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168...
Ejemplo: Calcular el m. c. m. de 4, 5 y 6.
Se hace la descomposición de factores (que ya la explicamos en el máximo común divisor). Lo hacemos de la siguiente forma:
4= 2x25= 56= 2x3
Se toman los factores comunes y no comunes con el mayor exponente y se multiplican: 2x2 x3 x5 = 60. El mcm de 4,5 y 6 es 60.
Ejemplo: Averiguar el m.c.m. de Sacar el M.C.D. de 20 y 10:
20:
20, 40, 60, 80...
10:
10, 20, 30...
20 es el múltiplo menor que es común a ambos números.
Multiplos: los múltiplos de un número se obtienen multiplicando dicho número por los números naturales 0, 1, 2, 3, 4, 5.....
Ejemplo: múltiplos del 7: 7x0=0; 7x1=7; 7x2=14; 7x3=21; 7x4=28; 7x5=35 ....
O sea son múltiplos del 7:, 0, 7, 14, 21, 28, 35, 42, 48, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168...
Ejemplo: Calcular el m. c. m. de 4, 5 y 6.
Se hace la descomposición de factores (que ya la explicamos en el máximo común divisor). Lo hacemos de la siguiente forma:
4= 2x25= 56= 2x3
Se toman los factores comunes y no comunes con el mayor exponente y se multiplican: 2x2 x3 x5 = 60. El mcm de 4,5 y 6 es 60.
Máximo Común Divisor (M.C.D.)
El máximo común divisor de dos o más números es el número, más grande posible, que permite dividir a esos números.
Para calcularlo. De los números que vayas a sacar el máximo común divisor, se ponen uno debajo del otro, se sacan todos los divisores de los dos números y el máximo que se repita es el máximo común divisor (M.C.D.)
Ejemplo: Sacar el M.C.D. de 20 y 10:
20:
1, 2, 4, 5, 10 y 20
10:
1, 2, 5 y 10
Esto sirve para números pequeños. Pero para números grandes hay otra manera: la descomposición de factores.
Forma rápida de calcular el Máximo común Divisor (M.C.D.).
Ejemplo: Sacar el M. C. D. de 40 y 60:
1º Tienes que saber las reglas divisibilidad. Haces la descomposición de factores poniendo números primos. Por ejemplo para 40, en la tabla de abajo, se va descomponiendo en 2, 2, 2 y 5.
2º De los resultados, se cogen los números repetidos de menor exponente y se multiplican y ese es el M.C.D.
40 = 2x2x2x5
60 = 2x2x3x5
MCD = 2x2x5= 20
Para calcularlo. De los números que vayas a sacar el máximo común divisor, se ponen uno debajo del otro, se sacan todos los divisores de los dos números y el máximo que se repita es el máximo común divisor (M.C.D.)
Ejemplo: Sacar el M.C.D. de 20 y 10:
20:
1, 2, 4, 5, 10 y 20
10:
1, 2, 5 y 10
Esto sirve para números pequeños. Pero para números grandes hay otra manera: la descomposición de factores.
Forma rápida de calcular el Máximo común Divisor (M.C.D.).
Ejemplo: Sacar el M. C. D. de 40 y 60:
1º Tienes que saber las reglas divisibilidad. Haces la descomposición de factores poniendo números primos. Por ejemplo para 40, en la tabla de abajo, se va descomponiendo en 2, 2, 2 y 5.
2º De los resultados, se cogen los números repetidos de menor exponente y se multiplican y ese es el M.C.D.
40 = 2x2x2x5
60 = 2x2x3x5
MCD = 2x2x5= 20
PROBLEMAS DE DIVISIBILIDAD
Primer problema
Un coche necesita que le cambien el aceite cada 9.000 km, el filtro del aire cada 15.000 km y las bujías cada 30.000 km. ¿ A qué número mínimo de kilómetros habrá que hacerle todos los cambios a la vez?
Solución
El coche realizará los siguientes cambios: De aceite: {9.000 Km., 18.000 Km., 27.000 Km, ...} Del filtro: {15.000 Km., 30.000 Km., 45.000 Km., ...} De bujías: {30.000 Km., 60.000 Km., 90.000 Km., ...} Comonpodemos comprobar los cambios se efectúan en múltiplos de 9.000, 15.000 y 30.000, como estamos buscando cuando se realizarán los tres cambios a la vez, estamos buscando un múltiplo común. Dado que también nos piden que el número buscado sea lo más pequeño posible, estamos buscando el M.C.M.(9.000,15.000,30.000)=90.000 Luego se realizarán los tres cambios simultáneamente por primera vez a los 90.000 Km.
Segundo problema
Un comerciante desea poner en cajas 12.028 manzanas y 12.772 naranjas de modo que cada caja contenga el mismo número de manzanas o de naranjas y además el mayor número posible de ellas. Hallar el número de naranjas y de manzanas de cada caja.
Solución
El comerciante puede poner las manzanas en cajas de 2 unidades, de 4 unidades, de 31 unidades, etc., en definitiva puede agruparlas en cajas que contengan cualquier divisor de 12.028. Igualmente ocurre con la naranjas, cajas de 2 unidades, de 4 unidades, etc, todos los divisores de 12.772. Puesto que el número de una caja de naranjas debe ser el mismo que el de una caja de manzanas, estamos buscando un divisor común, que además se nos pide que sea el mayor posible, este número es el M.C.D.(12.028,12.772)=124 Luego las cajas deben contener 124 unidades de naranjas o 124 unidades de nanzanas.
Un coche necesita que le cambien el aceite cada 9.000 km, el filtro del aire cada 15.000 km y las bujías cada 30.000 km. ¿ A qué número mínimo de kilómetros habrá que hacerle todos los cambios a la vez?
Solución
El coche realizará los siguientes cambios: De aceite: {9.000 Km., 18.000 Km., 27.000 Km, ...} Del filtro: {15.000 Km., 30.000 Km., 45.000 Km., ...} De bujías: {30.000 Km., 60.000 Km., 90.000 Km., ...} Comonpodemos comprobar los cambios se efectúan en múltiplos de 9.000, 15.000 y 30.000, como estamos buscando cuando se realizarán los tres cambios a la vez, estamos buscando un múltiplo común. Dado que también nos piden que el número buscado sea lo más pequeño posible, estamos buscando el M.C.M.(9.000,15.000,30.000)=90.000 Luego se realizarán los tres cambios simultáneamente por primera vez a los 90.000 Km.
Segundo problema
Un comerciante desea poner en cajas 12.028 manzanas y 12.772 naranjas de modo que cada caja contenga el mismo número de manzanas o de naranjas y además el mayor número posible de ellas. Hallar el número de naranjas y de manzanas de cada caja.
Solución
El comerciante puede poner las manzanas en cajas de 2 unidades, de 4 unidades, de 31 unidades, etc., en definitiva puede agruparlas en cajas que contengan cualquier divisor de 12.028. Igualmente ocurre con la naranjas, cajas de 2 unidades, de 4 unidades, etc, todos los divisores de 12.772. Puesto que el número de una caja de naranjas debe ser el mismo que el de una caja de manzanas, estamos buscando un divisor común, que además se nos pide que sea el mayor posible, este número es el M.C.D.(12.028,12.772)=124 Luego las cajas deben contener 124 unidades de naranjas o 124 unidades de nanzanas.
CRITERIOS DE DIVISIBILIDAD
Criterios de divisibilidad
Los criterios de divisibilidad son reglas que sirven para saber si un número es divisible por otro sin necesidad de realizar la división. Aunque pueden buscarse criterios para todos los números, sólo expondremos los más comunes:
Criterio de divisibilidad por 2
Un número es divisible por 2 si acaba en 0 o cifra par.
Ejemplos: Números divisibles por 2: 36,94,521342,40,...
Criterio de divisibilidad por 3
Un número es divisible por 3 si la suma de sus cifras es múltiplo de 3.
Ejemplos: Números divisibles por 3: 36,2142,42,...
Criterio de divisibilidad por 5
Un número es divisible por 5 si la última de sus cifras es 5 o es 0.
Ejemplos: Números divisibles por 5: 35,2145,40,...
Criterio de divisibilidad por 9
Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.
Ejemplos: Números divisibles por 9: 495,945,53640,...
Criterio de divisibilidad por 11
Debemos hacer lo siguiente: Sumamos las cifras que ocupan lugares pares, sumamos las cifras que ocupan lugares impares. A la suma mayor le restamos la suma menor, si la diferencia es 0 o múltiplo de 11, entonces el número es múltiplo de 11.
Ejemplos: Múltiplos de 11: 2343649,9889,18161902,...
Los criterios de divisibilidad son reglas que sirven para saber si un número es divisible por otro sin necesidad de realizar la división. Aunque pueden buscarse criterios para todos los números, sólo expondremos los más comunes:
Criterio de divisibilidad por 2
Un número es divisible por 2 si acaba en 0 o cifra par.
Ejemplos: Números divisibles por 2: 36,94,521342,40,...
Criterio de divisibilidad por 3
Un número es divisible por 3 si la suma de sus cifras es múltiplo de 3.
Ejemplos: Números divisibles por 3: 36,2142,42,...
Criterio de divisibilidad por 5
Un número es divisible por 5 si la última de sus cifras es 5 o es 0.
Ejemplos: Números divisibles por 5: 35,2145,40,...
Criterio de divisibilidad por 9
Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.
Ejemplos: Números divisibles por 9: 495,945,53640,...
Criterio de divisibilidad por 11
Debemos hacer lo siguiente: Sumamos las cifras que ocupan lugares pares, sumamos las cifras que ocupan lugares impares. A la suma mayor le restamos la suma menor, si la diferencia es 0 o múltiplo de 11, entonces el número es múltiplo de 11.
Ejemplos: Múltiplos de 11: 2343649,9889,18161902,...
OPERACIONES COMBINADAS
Las operaciones combinadas son aquellas en las que aparecen varias operaciones aritméticas para resolver.
Para obtener el resultado correcto deben seguirse las siguientes reglas:
- Se resuelven las operaciones encerradas entre paréntesis, corchetes y llaves en el siguiente orden:
1) Potenciación y radicación
2) Multiplicación y división
3) Suma y resta - Se resuelven las sumas y las restas que separan los términos.
Para obtener el resultado correcto deben seguirse las siguientes reglas:
- Se resuelven las operaciones encerradas entre paréntesis, corchetes y llaves en el siguiente orden:
1) Potenciación y radicación
2) Multiplicación y división
3) Suma y resta - Se resuelven las sumas y las restas que separan los términos.
martes, enero 23, 2007
Operaciones aritméticas
Suma o adición
La suma es una operación que se deriva de la operación de contar.
Si tenemos 6 ovejas y compramos 2 ovejas ¿cuantas ovejas tenemos?. Una forma de hacerlo sería volver a contar todas las ovejas, pero alguien que hubiese contado varias veces el mismo caso, recordaria el resultado y no necesitaría volver a contar las ovejas. Sabria que 6 + 2 = 8.
Los términos de la suma se llaman sumandos.
Propiedades de la suma:
a + b = b + a Esta propiedad se llama conmutativa.
Si tenemos que sumar varios numeros podemos hacerlo en cualquier orden (esto se llama propiedad asociativa). Si tenemos que sumar a, b, c y d, podemos sumar primero a + b, despues c + d y despues sumar los dos resultados anteriores, o podemos sumar a + c, despues b + d y despues sumar los dos resultados anteriores o podemos sumar a + b y al resultado sumarle c y al resultado sumarle d. En fin podemos sumar los numeros en cualquier orden.
La suma tiene elemento neutro. El cero es el elemento neutro de la suma porque siempre se cumple que a + 0 = a.
La suma tiene elemento simétrico. El elemento simetrico de un número es otro que sumado al anterior da el elemento neutro. El elemento simetrico de a es -a, porque a + (-a) = 0
Resta o substración
Igual que la suma la resta es una operacion que se deriva de la operacion de contar.
Si tenemos 6 ovejas y los lobos se comen 2 ovejas ¿cuantas ovejas tenemos?. Una forma de hacerlo sería volver a contar todas las ovejas, pero alguien que hubiese contado varias veces el mismo caso, recordaria el resultado y no necesitaría volver a contar las ovejas. Sabria que 6 - 2 = 4.
Los terminos de la resta se llaman minuendo (las ovejas que tenemos) y sustraendo (las ovejas que se comieron los lobos).
Propiedades de la resta:
La resta no tiene la propiedad conmutativa (no es lo mismo a - b que b - a)
Producto o multiplicación
Muchas veces tenemos que sumar un número consigo mismo varias veces. Por ejemplo, si tenemos que sumar 5 + 5 + 5 + 5 + 5 + 5 + 5, sería más breve representarlo asi 5 * 7 (esto significaria sumar 5 condigo mismo 7 veces).
La multiplicación es una forma abreviada de hacer un tipo especial de sumas.
Los terminos de la multiplicación se llaman multiplicando (el numero que se suma) y multiplicador (el número de veces que se suma).
Propiedades de la multiplicación
a * b = b * a. Esta propiedad se llama propiedad conmutativa
Si tenemos que multiplicar varios numeros podemos hacerlo en cualquier orden (esto se llama propiedad asociativa). Si tenemos que multiplicar a, b, c y d, podemos multiplicar primero a . b, despues c . d y despues multiplicar los dos resultados anteriores, o podemos multiplicar a . c, despues b . d y despues multiplicar los dos resultados anteriores o podemos multiplicar a . b y multiplicar el resultado por c y despues multiplicarlo por d. En fin podemos multiplicar los numeros en cualquier orden.
La multiplicación tiene elemento neutro. El uno es el elemento neutro de la multiplicación porque siempre se cumple que a .1 = a.
La multiplicación tiene elemento simétrico. El elemento simetrico de un número es otro que multiplicado por el anterior da el elemento neutro. El elemento simetrico de a es 1/a, porque a / a = 0
a(b + c) = a . c + a . d. Esta propiedad se llama distributiva respecto a la suma.
División
La división es la operación que tenemos que hacer para repartir un numero de cosas entre un número de personas.
Los terminos de la división se llaman dividendo (el número de cosas), divisor (el número de personas), cociente (el numero que le corresponde a cada persona) y resto (lo que sobra).
Si el resto es cero la división se llama exacta y en caso contrario inexacta.
Propiedades de la division
La divisón no tiene la propiedad conmutativa. No es lo mismo a/b que b/a.
Potenciación
En bastantes ocasiones tenemos que multiplicar un número por si mismo un número dado de veces.
Por ejemplo: 5 * 5 * 5 * 5 * 5 * 5 * 5
Una forma de representar esta operacion es 57 (esto quiere decir que hay que multiplicar 5 por si mismo 7 veces).
El numero inferior se llama base y el superior exponente.
Propiedades de la potenciación:
am.an = am+n
am/an = am-n
a0 = 1 (se deriva de la propiedad anterior am/am = 1 = am-m = a0)
(am)n = am.n
(a.b.c)m = am . bm .cm
a-n = 1/an (se deriva de la segunda propiedad).
Radicación
La radicacion es la operacion inversa de la potenciación. Supongamos que nos dan un número a y nos piden calcular otro, tal que, multiplicado por si mismo un número b de veces nos da el numero a.
Por ejemplo: calcular qué número multiplicado por si mismo 2 veces da 196. Ese número es 14.
El número que esta dentro de la raiz se llama radicando, el grado de la raiz se llama índice del radical, el resultado se llama raiz.
Podemos considerar la radicación como un caso particular de la potenciación. En efecto, la raiz cuadrada de un numero (por ejemplo a) es igual que a1/2, del mismo modo la raiz cúbica de a es a1/3 y en general, la raiz enesima de un numero a es a1/n.
La mejor forma de resolver los ejercicios de operaciones con raices es convertir las raices a potencias y operar teneiendo en cuenta las propiedades dadas para la operacion de potenciación.
Raiz cuadrada
1- Para calcular la raiz cuadrada de un número se comienza separando el numero en grupos de dos cifras, empezando por la derecha
Por ejemplo: 5560164 lo separaríamos 5'56'01'64
2- A continuacion se calcula un numero entero que elevado al cuadrado sea igual (o lo mas proximo al numero del primer grupo, empezando por la izquierda).
En nuestro ejemplo el primer numero es 5 y el numero entero que elevado al cuadrado se acerca mas a 5 es 2. 2 es la primera cifra de la raiz.
3- Despues se eleva al cuadrado esta cifra y se resta del numero del primer grupo
En nuestro ejemplo 22 = 4 y restandolo del numero del primer grupo que es 5, sale 5 -4 = 1
4- A continuacion ponemos al lado del resto anterior el numero del siguiente grupo
En nuestro ejemplo nos quedaria 156
5- Despues multiplicamos por 2 el numero que hemos calculado hasta el momento de la raiz.
En nuestro ejemplo seria 2 * 2 = 4
6- A continuacion tenemos que buscar un numero que multiplicado por el numero que resulta de multiplicar por 10 el numero anterior y sumarle el numero quee stamos buscando se acerque lo mas posible al numero que tenemos como resto. Ese numero sera el siguiente numero de la raiz.
En nuestro ejemplo el numero seria 3 porque 43 * 3 = 129 que es el numero que se aproxima mas a 156 y la raiz seria 23...
7- Ahora tenemos que volver a calcular el resto restando el numero obtenido del que queriamos obtener realmente.
En nuetro ejemplo: 156 - 129 = 27
8- A continuacion repetimos el paso 4, esto es, ponemos al lado del resto anterior el numero del siguiente grupo
En nuestro ejemplo: 2701
9- A continuación repetimos el paso 5
En nuestro ejemplo: 23 * 2 = 46
10- Despues repetimos el paso 6
En nuestro ejemplo el numero seria 5 porque 465 *5 = 2325 que es el numero que se aproxima mas a 2701 y la raiz seria 235...
11- Despues repetimos el paso 7
En nuetro ejemplo: 2701 - 2325 = 376
12- A continuacion repetimos el paso 8
En nuestro ejemplo: 37664
13 A continuacion repetimos el paso 5
En nuestro ejemplo seria 235 * 2 = 470
14- A continuacion repetimos el paso 6
En nuestro ejemplo el numero seria 8 porque 4708 * 8 = 37664 que es el numero que se aproxima mas a 37664 y la raiz seria 2358
15- A continuacion repetimos el paso 7
En nuestro ejemplo: 37664 - 37664 = 0 En este caso la raiz es exacta pues el resto es cero.
Raiz cubica
1- Para calcular la raiz cúbica de un número se comienza separando el numero en grupos de tres cifras, empezando por la derecha
Por ejemplo: 16387064 lo separaríamos 16'387'064
2- A continuacion se calcula un numero entero que elevado al cubo se aproxime lo mas posible al numero del primer grupo (empezando por la izquierda).
En nuestro ejemplo el primer numero es 16 y el numero entero que elevado al cubo se acerca mas a 16 es 2. 2 es la primera cifra de la raiz.
3- Despues se eleva al cubo esta cifra y se resta del numero del primer grupo
En nuestro ejemplo 23 = 8 y restandolo del numero del primer grupo que es 16, sale 16 - 8 = 8
4- A continuacion ponemos al lado del resto anterior el numero del siguiente grupo.
En nuestro ejemplo nos quedaria 8387
5- Despues tenemos que calcular un numero a que haciendo las operaciones siguientes:
3 * (raiz obtenida hasta el momento)2 * a * 100 + 3 * (raiz obtenida hasta el momento) * a2 * 10 + a3
se aproxime lo mas posible al numero obtenido en el punto 4.
El número a, es el siguiente dígito de la raiz.
En nuestro ejemplo seria ese número sería 5, porque 3 * 22 * 5 * 100 + 3 * 2 * 52 *10 + 53 = 7625
6- A continuacion restamos este numero al numero obtenido en el paso 4.
En nuestro ejemplo: 8387 - 7625 = 762.
7- Repetimos el paso 4
En nuestro ejemplo: 762064
8- Repetimos el paso 5 y el numero obtenido seria el siguiente numero de la raiz.
En el ejemplo sería el 4 porque 3 * 252 * 4 * 100 + 3 * 25 * 42 *10 + 43 = 762064
9 Repetimos el paso 6
En nuestro ejemplo 762064 - 762064 = 0
La suma es una operación que se deriva de la operación de contar.
Si tenemos 6 ovejas y compramos 2 ovejas ¿cuantas ovejas tenemos?. Una forma de hacerlo sería volver a contar todas las ovejas, pero alguien que hubiese contado varias veces el mismo caso, recordaria el resultado y no necesitaría volver a contar las ovejas. Sabria que 6 + 2 = 8.
Los términos de la suma se llaman sumandos.
Propiedades de la suma:
a + b = b + a Esta propiedad se llama conmutativa.
Si tenemos que sumar varios numeros podemos hacerlo en cualquier orden (esto se llama propiedad asociativa). Si tenemos que sumar a, b, c y d, podemos sumar primero a + b, despues c + d y despues sumar los dos resultados anteriores, o podemos sumar a + c, despues b + d y despues sumar los dos resultados anteriores o podemos sumar a + b y al resultado sumarle c y al resultado sumarle d. En fin podemos sumar los numeros en cualquier orden.
La suma tiene elemento neutro. El cero es el elemento neutro de la suma porque siempre se cumple que a + 0 = a.
La suma tiene elemento simétrico. El elemento simetrico de un número es otro que sumado al anterior da el elemento neutro. El elemento simetrico de a es -a, porque a + (-a) = 0
Resta o substración
Igual que la suma la resta es una operacion que se deriva de la operacion de contar.
Si tenemos 6 ovejas y los lobos se comen 2 ovejas ¿cuantas ovejas tenemos?. Una forma de hacerlo sería volver a contar todas las ovejas, pero alguien que hubiese contado varias veces el mismo caso, recordaria el resultado y no necesitaría volver a contar las ovejas. Sabria que 6 - 2 = 4.
Los terminos de la resta se llaman minuendo (las ovejas que tenemos) y sustraendo (las ovejas que se comieron los lobos).
Propiedades de la resta:
La resta no tiene la propiedad conmutativa (no es lo mismo a - b que b - a)
Producto o multiplicación
Muchas veces tenemos que sumar un número consigo mismo varias veces. Por ejemplo, si tenemos que sumar 5 + 5 + 5 + 5 + 5 + 5 + 5, sería más breve representarlo asi 5 * 7 (esto significaria sumar 5 condigo mismo 7 veces).
La multiplicación es una forma abreviada de hacer un tipo especial de sumas.
Los terminos de la multiplicación se llaman multiplicando (el numero que se suma) y multiplicador (el número de veces que se suma).
Propiedades de la multiplicación
a * b = b * a. Esta propiedad se llama propiedad conmutativa
Si tenemos que multiplicar varios numeros podemos hacerlo en cualquier orden (esto se llama propiedad asociativa). Si tenemos que multiplicar a, b, c y d, podemos multiplicar primero a . b, despues c . d y despues multiplicar los dos resultados anteriores, o podemos multiplicar a . c, despues b . d y despues multiplicar los dos resultados anteriores o podemos multiplicar a . b y multiplicar el resultado por c y despues multiplicarlo por d. En fin podemos multiplicar los numeros en cualquier orden.
La multiplicación tiene elemento neutro. El uno es el elemento neutro de la multiplicación porque siempre se cumple que a .1 = a.
La multiplicación tiene elemento simétrico. El elemento simetrico de un número es otro que multiplicado por el anterior da el elemento neutro. El elemento simetrico de a es 1/a, porque a / a = 0
a(b + c) = a . c + a . d. Esta propiedad se llama distributiva respecto a la suma.
División
La división es la operación que tenemos que hacer para repartir un numero de cosas entre un número de personas.
Los terminos de la división se llaman dividendo (el número de cosas), divisor (el número de personas), cociente (el numero que le corresponde a cada persona) y resto (lo que sobra).
Si el resto es cero la división se llama exacta y en caso contrario inexacta.
Propiedades de la division
La divisón no tiene la propiedad conmutativa. No es lo mismo a/b que b/a.
Potenciación
En bastantes ocasiones tenemos que multiplicar un número por si mismo un número dado de veces.
Por ejemplo: 5 * 5 * 5 * 5 * 5 * 5 * 5
Una forma de representar esta operacion es 57 (esto quiere decir que hay que multiplicar 5 por si mismo 7 veces).
El numero inferior se llama base y el superior exponente.
Propiedades de la potenciación:
am.an = am+n
am/an = am-n
a0 = 1 (se deriva de la propiedad anterior am/am = 1 = am-m = a0)
(am)n = am.n
(a.b.c)m = am . bm .cm
a-n = 1/an (se deriva de la segunda propiedad).
Radicación
La radicacion es la operacion inversa de la potenciación. Supongamos que nos dan un número a y nos piden calcular otro, tal que, multiplicado por si mismo un número b de veces nos da el numero a.
Por ejemplo: calcular qué número multiplicado por si mismo 2 veces da 196. Ese número es 14.
El número que esta dentro de la raiz se llama radicando, el grado de la raiz se llama índice del radical, el resultado se llama raiz.
Podemos considerar la radicación como un caso particular de la potenciación. En efecto, la raiz cuadrada de un numero (por ejemplo a) es igual que a1/2, del mismo modo la raiz cúbica de a es a1/3 y en general, la raiz enesima de un numero a es a1/n.
La mejor forma de resolver los ejercicios de operaciones con raices es convertir las raices a potencias y operar teneiendo en cuenta las propiedades dadas para la operacion de potenciación.
Raiz cuadrada
1- Para calcular la raiz cuadrada de un número se comienza separando el numero en grupos de dos cifras, empezando por la derecha
Por ejemplo: 5560164 lo separaríamos 5'56'01'64
2- A continuacion se calcula un numero entero que elevado al cuadrado sea igual (o lo mas proximo al numero del primer grupo, empezando por la izquierda).
En nuestro ejemplo el primer numero es 5 y el numero entero que elevado al cuadrado se acerca mas a 5 es 2. 2 es la primera cifra de la raiz.
3- Despues se eleva al cuadrado esta cifra y se resta del numero del primer grupo
En nuestro ejemplo 22 = 4 y restandolo del numero del primer grupo que es 5, sale 5 -4 = 1
4- A continuacion ponemos al lado del resto anterior el numero del siguiente grupo
En nuestro ejemplo nos quedaria 156
5- Despues multiplicamos por 2 el numero que hemos calculado hasta el momento de la raiz.
En nuestro ejemplo seria 2 * 2 = 4
6- A continuacion tenemos que buscar un numero que multiplicado por el numero que resulta de multiplicar por 10 el numero anterior y sumarle el numero quee stamos buscando se acerque lo mas posible al numero que tenemos como resto. Ese numero sera el siguiente numero de la raiz.
En nuestro ejemplo el numero seria 3 porque 43 * 3 = 129 que es el numero que se aproxima mas a 156 y la raiz seria 23...
7- Ahora tenemos que volver a calcular el resto restando el numero obtenido del que queriamos obtener realmente.
En nuetro ejemplo: 156 - 129 = 27
8- A continuacion repetimos el paso 4, esto es, ponemos al lado del resto anterior el numero del siguiente grupo
En nuestro ejemplo: 2701
9- A continuación repetimos el paso 5
En nuestro ejemplo: 23 * 2 = 46
10- Despues repetimos el paso 6
En nuestro ejemplo el numero seria 5 porque 465 *5 = 2325 que es el numero que se aproxima mas a 2701 y la raiz seria 235...
11- Despues repetimos el paso 7
En nuetro ejemplo: 2701 - 2325 = 376
12- A continuacion repetimos el paso 8
En nuestro ejemplo: 37664
13 A continuacion repetimos el paso 5
En nuestro ejemplo seria 235 * 2 = 470
14- A continuacion repetimos el paso 6
En nuestro ejemplo el numero seria 8 porque 4708 * 8 = 37664 que es el numero que se aproxima mas a 37664 y la raiz seria 2358
15- A continuacion repetimos el paso 7
En nuestro ejemplo: 37664 - 37664 = 0 En este caso la raiz es exacta pues el resto es cero.
Raiz cubica
1- Para calcular la raiz cúbica de un número se comienza separando el numero en grupos de tres cifras, empezando por la derecha
Por ejemplo: 16387064 lo separaríamos 16'387'064
2- A continuacion se calcula un numero entero que elevado al cubo se aproxime lo mas posible al numero del primer grupo (empezando por la izquierda).
En nuestro ejemplo el primer numero es 16 y el numero entero que elevado al cubo se acerca mas a 16 es 2. 2 es la primera cifra de la raiz.
3- Despues se eleva al cubo esta cifra y se resta del numero del primer grupo
En nuestro ejemplo 23 = 8 y restandolo del numero del primer grupo que es 16, sale 16 - 8 = 8
4- A continuacion ponemos al lado del resto anterior el numero del siguiente grupo.
En nuestro ejemplo nos quedaria 8387
5- Despues tenemos que calcular un numero a que haciendo las operaciones siguientes:
3 * (raiz obtenida hasta el momento)2 * a * 100 + 3 * (raiz obtenida hasta el momento) * a2 * 10 + a3
se aproxime lo mas posible al numero obtenido en el punto 4.
El número a, es el siguiente dígito de la raiz.
En nuestro ejemplo seria ese número sería 5, porque 3 * 22 * 5 * 100 + 3 * 2 * 52 *10 + 53 = 7625
6- A continuacion restamos este numero al numero obtenido en el paso 4.
En nuestro ejemplo: 8387 - 7625 = 762.
7- Repetimos el paso 4
En nuestro ejemplo: 762064
8- Repetimos el paso 5 y el numero obtenido seria el siguiente numero de la raiz.
En el ejemplo sería el 4 porque 3 * 252 * 4 * 100 + 3 * 25 * 42 *10 + 43 = 762064
9 Repetimos el paso 6
En nuestro ejemplo 762064 - 762064 = 0
NÚMEROS ENTEROS
1º) 63-84=
2º) (+34) - ( -25 ) =
3º) ( -48) - ( -52) =
4º) ( + 75 ) - ( - 39 ) =
5º) 256- ( + 256 ) =
6º) ( -4 ) - ( + 12 ) =
7º) 68- ( 21 - 54 ) + ( 7 - 72 ) =
8º) - ( 24 - 89 + 18 ) + ( - 91 + 24 ) =
9º) - ( - 417 - 78 ) - ( -518- 287 ) =
10º) 14 + [ 23 - ( 34 - 57 ) ] =
11º) 14 - [ 23 - ( 34 - 57 ) ] =
12º) - 32 - [ 19- ( 24 - 46 ) ] =
13º) ( - 3 ) ( - 6 ) ( + 4 ) =
14º) ( -8 ) ( - 3 ) ( - 7 ) =
15º) ( - 6 ) 8 ( - 10 ) =
16º) - 14 + 3 ( - 8 ) =
17º) 29 [(-10) + 1 ] =
18º) 12 [ 40 + ( - 3 ) ] =
19º) ( 4 - 20) 13 =
20º) (- 5 ) . 7 - 9 ( - 4 ) =
21º) -13 - ( - 3 ) ( - 9 ) + 5 ( - 8 ) =
22º) (- 48 + 32 ) - ( 67 - 82 ) =
23º) 48 - [ 15 - ( 43 - 38 ) - 27 ] =
24º) - [ - 13 + ( 24 - 68 ) ] - ( - 48 + 95 ) =
25º) (-12 ) . 7 - 13 ( - 5 ) =
26º) 12 ( - 7 ) - 12 =
27º) (- 13 ) 3 =
28º) 8 ( - 11 ) =
2º) (+34) - ( -25 ) =
3º) ( -48) - ( -52) =
4º) ( + 75 ) - ( - 39 ) =
5º) 256- ( + 256 ) =
6º) ( -4 ) - ( + 12 ) =
7º) 68- ( 21 - 54 ) + ( 7 - 72 ) =
8º) - ( 24 - 89 + 18 ) + ( - 91 + 24 ) =
9º) - ( - 417 - 78 ) - ( -518- 287 ) =
10º) 14 + [ 23 - ( 34 - 57 ) ] =
11º) 14 - [ 23 - ( 34 - 57 ) ] =
12º) - 32 - [ 19- ( 24 - 46 ) ] =
13º) ( - 3 ) ( - 6 ) ( + 4 ) =
14º) ( -8 ) ( - 3 ) ( - 7 ) =
15º) ( - 6 ) 8 ( - 10 ) =
16º) - 14 + 3 ( - 8 ) =
17º) 29 [(-10) + 1 ] =
18º) 12 [ 40 + ( - 3 ) ] =
19º) ( 4 - 20) 13 =
20º) (- 5 ) . 7 - 9 ( - 4 ) =
21º) -13 - ( - 3 ) ( - 9 ) + 5 ( - 8 ) =
22º) (- 48 + 32 ) - ( 67 - 82 ) =
23º) 48 - [ 15 - ( 43 - 38 ) - 27 ] =
24º) - [ - 13 + ( 24 - 68 ) ] - ( - 48 + 95 ) =
25º) (-12 ) . 7 - 13 ( - 5 ) =
26º) 12 ( - 7 ) - 12 =
27º) (- 13 ) 3 =
28º) 8 ( - 11 ) =
NÚMEROS NATURALES
1º) 4+2.3=
2º) 3.2-4=
3º) 12-3.2+2.3-4.3=
4º) 6-3.0=
5º) 3.(2+4.3) - 2.( 3.2-2.2) + 5 -2 =
6º) 8:2 + 4.2 - 3: 1 =
7º) 5. ( 6 + 3.2 -4) - ( 3.1 + 2.5 -3 ) =
8º) 2.( ( 21-11) 2- 6.3 ) - 4.0 =
9º) 2[ 5 - 3.1 + 2 ( + 3 - 2 ) . 3 ] - 5 =
10º) [ ( 5 - 2 ). ( 6 - 3 ) ] : ( 2 + 1 ) =
11º) ( 6 - 6 ) . [ 15 - 2 . ( 6 - 2 . 2 ) ]=
12º) 3 . [ 15 - 2 ( 6 - 2 . 2 )] =
2º) 3.2-4=
3º) 12-3.2+2.3-4.3=
4º) 6-3.0=
5º) 3.(2+4.3) - 2.( 3.2-2.2) + 5 -2 =
6º) 8:2 + 4.2 - 3: 1 =
7º) 5. ( 6 + 3.2 -4) - ( 3.1 + 2.5 -3 ) =
8º) 2.( ( 21-11) 2- 6.3 ) - 4.0 =
9º) 2[ 5 - 3.1 + 2 ( + 3 - 2 ) . 3 ] - 5 =
10º) [ ( 5 - 2 ). ( 6 - 3 ) ] : ( 2 + 1 ) =
11º) ( 6 - 6 ) . [ 15 - 2 . ( 6 - 2 . 2 ) ]=
12º) 3 . [ 15 - 2 ( 6 - 2 . 2 )] =
ECUACIONES
7 + 2x = 13
15 + 7x = 1
4x – 3 = 2x
5x – 3 = 1 – 2x
(x/2)+5 = (x/3)+6
5x – 20 = x+8
(x+6)/2 = 2x – 21
(2x–3)/(4x–3) = 1
2/(3–x) + 1/(2+x) = 0
(x+10)/(3x+5) = 2
(11x+1)/(6x–2) = 2
(x+2)(x+3) = (x+1)(x+7)
15 + 7x = 1
4x – 3 = 2x
5x – 3 = 1 – 2x
(x/2)+5 = (x/3)+6
5x – 20 = x+8
(x+6)/2 = 2x – 21
(2x–3)/(4x–3) = 1
2/(3–x) + 1/(2+x) = 0
(x+10)/(3x+5) = 2
(11x+1)/(6x–2) = 2
(x+2)(x+3) = (x+1)(x+7)
ECUACIONES
5+x = 7
x/2 = 3
x/3 + 4 = 8
4x – 5 = 15
3x + 6 = 5x
6x + 4 = 1.5x + 13
15x – 2 = 6x + 16
21x – 3 = (7x+9)/2
x/2 = 3
x/3 + 4 = 8
4x – 5 = 15
3x + 6 = 5x
6x + 4 = 1.5x + 13
15x – 2 = 6x + 16
21x – 3 = (7x+9)/2
lunes, enero 22, 2007
GLOSARIO
ángulo agudo
un ángulo que mide menos de 90°
ángulo
la reunión de dos rayos que tienen un mismo punto de origen y no están en la misma recta
ángulo obtuso
un ángulo que mide más de 90°
ángulo recto
un ángulo que mide 90°
área
cantidad de superfície dentro de una estructura
cuadrado
rectángulo con lados congruentes y ángulos de 90°
cuadrilátero
un polígono de cuatro lados
cuerda
un segmento cuyos puntos finales están en un círculo
circunferencia
distancia alrededor de un círculo
espacio
el conjunto de todos los puntos
diámetro
una cuerda que pasa por el centro de un círculo
perímetro
la distancia alrededor de una figura plana
pi
la razón de la circunferencia de un círculo a su diámetro. Redondeado equivale a 3.14
polígono
una figura cerrada cuyos lados son líneas rectas
radio
En una circunferencia, segmento que une cualquiera de sus puntos con el centro.
simétríca
figura que , cuando se dobla por una línea de simetría tiene dos mitades iguales.
triángulo
figura de tres lados en un plano
vértice
punto común entre dos rayos que forman un ángulo
un ángulo que mide menos de 90°
ángulo
la reunión de dos rayos que tienen un mismo punto de origen y no están en la misma recta
ángulo obtuso
un ángulo que mide más de 90°
ángulo recto
un ángulo que mide 90°
área
cantidad de superfície dentro de una estructura
cuadrado
rectángulo con lados congruentes y ángulos de 90°
cuadrilátero
un polígono de cuatro lados
cuerda
un segmento cuyos puntos finales están en un círculo
circunferencia
distancia alrededor de un círculo
espacio
el conjunto de todos los puntos
diámetro
una cuerda que pasa por el centro de un círculo
perímetro
la distancia alrededor de una figura plana
pi
la razón de la circunferencia de un círculo a su diámetro. Redondeado equivale a 3.14
polígono
una figura cerrada cuyos lados son líneas rectas
radio
En una circunferencia, segmento que une cualquiera de sus puntos con el centro.
simétríca
figura que , cuando se dobla por una línea de simetría tiene dos mitades iguales.
triángulo
figura de tres lados en un plano
vértice
punto común entre dos rayos que forman un ángulo
Términos matemáticos
Álgebra: Viene del título de la obra del mátematico árabe al-Khowarizmi, al-jebr w'al-muqabalah. El significado orginal de al-jebr es 'reunión de partes rotas'
Axioma: cuestión que no necesita demostración
La palabra cálculo viene del latín calculi (guijarros), pues se utilizaban para facilitar los cálculos.
Conjetura: cuestión que no está demostrada pero que se intuye que es cierta.
Cuestión abierta: cuestión que no está demostrada.
El término escalar fue introducido por Hamilton.
El término función aparece por primera vez en un manuscrito de Leibniz de 1673.
Geometría tiene su origen en 'medir la tierra'.
Googol. Esta palabra representa el número 10100. Edward Kasner, un matemático americano, pidió a su sobrino de 9 años, que inventase una palabra para representar el número 10100.
Hiperbola: Este término se debe a Apolonio, que estudió las tres secciones cónicas.
Hipotenusa: Fue usado por Pitagoras.
Integral: Jacob Bernoulli fue el primero en usar el término integral
El término límite fue usado por Isaac Newton en 1727 Opuscula I
Logaritmo fue usado por primera vez por Napier en 1614 en Mirfici Logarithmorum Canonis descriptio.
El término mantisa fue introducido por Henry Briggs en 1624 en Arithmetica logarithmica. No se sabe si el término fue utilizado para significar la parte decimal de un logaritmo o la parte decimal de cualquier número. En 1696 John wallis lo utiliza para referirse a la parte decimal de un número. Leonahard Euler utiliza el término para referirse a la parte decimal de un logarítmo en Introductio in analysin infinitorum.
El término matriz fue acuñado en 1850 por James Joseph Sylvester.
El término millón aparece en 1494 en Summa de Arithmetica de Luca Paciola.
El término módulo (en teoria de números) fue introducido por Gauss y en número complejos por Augustin-Louis Cauchy.
El nombre de números trascendentes se debe a Euler porque estos números "trascienden el poderío de los métodos algebraicos".
El término número Real fue usado por primera vez por Descartes en 1637.
El término número perfecto, fue usado por Pitagoras. En ingles aparece por primera vez en la traducción de los Elementos de Euclides de Sir Henry Billinsley.
El término número primo, fue usado por Pitagoras. En ingles aparece por primera vez en la traducción de los Elementos de Euclides de Sir Henry Billinsley.
Obtuso (ángulo obtuso): Aparece por primera vez en una traducción de los Elementos de Euclides de Sir Henry Billingsley.
Postulado: proposición no evidente que se admite sin probar. Por ejemplo el 5º postulado dice "Por un punto exterior a una recta, solo puede trazarse una paralela a ésta")
Q.E.D: Significa quod erat demonstrandum (como queriamos demostrar). Euclides finalizaba sus demostraciones con esta frase.
El término Ratio fue usado por primera vez en 1660 por Isaac Barrow en Euclid.
El término raíz: fue introducido por al-Khowarizmi.
Teorema: es una proposición no evidente que se demuestra a partir de los axiomas y postulados.
Teorema: aparece en 1551 en The Pathway to Knowledge de Robert Recorde.
El término trigonometría fue introducido en 1595 por Bartholomeo Pitiscus en Trigonometria.
El término variable fue introducido por Leibniz
El término vector fue introducido por Hamilton.
Axioma: cuestión que no necesita demostración
La palabra cálculo viene del latín calculi (guijarros), pues se utilizaban para facilitar los cálculos.
Conjetura: cuestión que no está demostrada pero que se intuye que es cierta.
Cuestión abierta: cuestión que no está demostrada.
El término escalar fue introducido por Hamilton.
El término función aparece por primera vez en un manuscrito de Leibniz de 1673.
Geometría tiene su origen en 'medir la tierra'.
Googol. Esta palabra representa el número 10100. Edward Kasner, un matemático americano, pidió a su sobrino de 9 años, que inventase una palabra para representar el número 10100.
Hiperbola: Este término se debe a Apolonio, que estudió las tres secciones cónicas.
Hipotenusa: Fue usado por Pitagoras.
Integral: Jacob Bernoulli fue el primero en usar el término integral
El término límite fue usado por Isaac Newton en 1727 Opuscula I
Logaritmo fue usado por primera vez por Napier en 1614 en Mirfici Logarithmorum Canonis descriptio.
El término mantisa fue introducido por Henry Briggs en 1624 en Arithmetica logarithmica. No se sabe si el término fue utilizado para significar la parte decimal de un logaritmo o la parte decimal de cualquier número. En 1696 John wallis lo utiliza para referirse a la parte decimal de un número. Leonahard Euler utiliza el término para referirse a la parte decimal de un logarítmo en Introductio in analysin infinitorum.
El término matriz fue acuñado en 1850 por James Joseph Sylvester.
El término millón aparece en 1494 en Summa de Arithmetica de Luca Paciola.
El término módulo (en teoria de números) fue introducido por Gauss y en número complejos por Augustin-Louis Cauchy.
El nombre de números trascendentes se debe a Euler porque estos números "trascienden el poderío de los métodos algebraicos".
El término número Real fue usado por primera vez por Descartes en 1637.
El término número perfecto, fue usado por Pitagoras. En ingles aparece por primera vez en la traducción de los Elementos de Euclides de Sir Henry Billinsley.
El término número primo, fue usado por Pitagoras. En ingles aparece por primera vez en la traducción de los Elementos de Euclides de Sir Henry Billinsley.
Obtuso (ángulo obtuso): Aparece por primera vez en una traducción de los Elementos de Euclides de Sir Henry Billingsley.
Postulado: proposición no evidente que se admite sin probar. Por ejemplo el 5º postulado dice "Por un punto exterior a una recta, solo puede trazarse una paralela a ésta")
Q.E.D: Significa quod erat demonstrandum (como queriamos demostrar). Euclides finalizaba sus demostraciones con esta frase.
El término Ratio fue usado por primera vez en 1660 por Isaac Barrow en Euclid.
El término raíz: fue introducido por al-Khowarizmi.
Teorema: es una proposición no evidente que se demuestra a partir de los axiomas y postulados.
Teorema: aparece en 1551 en The Pathway to Knowledge de Robert Recorde.
El término trigonometría fue introducido en 1595 por Bartholomeo Pitiscus en Trigonometria.
El término variable fue introducido por Leibniz
El término vector fue introducido por Hamilton.
Símbolos matemáticos
Símbolos de relación:
Antiguamente se utilizaban palabras para referirse a los símbolos, por ejemplo para el signo igual se utilizaba aequales, aequantur, o abrevituras como aeq. El símbolo = aparece por primera vez en The Whetstone of whitte (El aguzador del ingenio) publicada en 1557 por Robert Recorde, que es el primer tratado inglés de álgebra. El autor afirma que eligió ese símbolo porque dos cosas no pueden ser más iguales que dos rectas paralelas. Este símbolo se generalizó hacia finales del siglo XVII; todavía en este siglo Descartes utiliza un signo semejante al símbolo del infinito, probable corrupción de la inicial de la palabra ae qualis (igual en latín).
Los símbolos <, > se deben a Thomas Harriot. Los utilizó en su libro póstumo Artis Analyticae Praxis ad aequationes Algebraicas Resolvendas.
Los símbolos actuales para representar, no igual, no mayor que, no menor que, se deben a Euler.
El símbolo :: fue introducido por William Oughtred en su libro Clavis Mathematicae (1631). Oughtred escribía las proporciones asi: a.b::c.d
La notación actual de las proporciones (a:b::c:d) se debe al astronomo Vincent Wing (1619-1668).
Simbolos de operaciones:
El símbolo x para la multiplicación parece ser original de Oughtred.
El símbolo . para la multiplicación fue utilizado por Thomas Harriot, pero quien lo popularizó fue Leibniz.
El símbolo Ö para la raíz, aparece por primera vez en el primer álgebra publicada en alemán vulgar, en 1525, de Christoff Rudolff.
Símbolos de constantes:
El símbolo p fue usado en 1647 por William Oughtred, para representar la circunferencia de un círculo. William Jones en 1706 en Sypnosis palmariorum mathesios, fue quien primero lo utilizó para la relación entre la longitud de la circunferencia y el diámetro. Sin embargo fue Leonhard Euler quien lo popularizó en 1748 en Introductio in Analysin Infinitorum.
El símbolo e fue usado por Leonhard Euler en el manuscrito Meditatio in Experimenta explosione tormentorum nuper instituta (Meditaciones sobre experimentos hechos recientemente sobre el fuego de un cañón) escrito en 1728.
El símbolo i, para la unidad imaginaria, fue usado por primera vez por Leonhard Euler en 1777 en Institutionum calculi integralis.
El símbolo f para la relacion aurea fue elegido por el matemático americano Mark Barr. La letra fue elegida porque era la primera letra del nombre de Phidias que solia usar la relacion aurea en sus esculturas.
Símbolos de números:
El símbolo 0 (cero) es muy reciente; recuerdese que los romanos no tenían un símbolo para representar el cero.
Parece ser que el cero se utilizaba en la India antes del nacimiento de Jesucristo, pero no hay ninguna evidencia escrita hasta mucho despues, en cualquier caso hay muchas evidencias que indican que el símbolo del cero surgió en la India.
Se discute si el símbolo que utilizaba Ptolomeo (la letra griega ómicron) representaba el cero.
El primer matemático europeo que defendió el uso del cero fue Leonardo de Pisa (más conocido por Fibonacci) en su libor Liber Abaci. Llamó al símbolo zephirum.
Símbolos de variables:
Diofanto usaba una letra griega con acento para representar una cantidad desconocida.
En la Edad Media se utilizaban palabras para representar cantidades desconocidas:
cosa = x
census = x2
cubo = x3
censo di censo = x4
cubo relato cosa = x5
cubo di cubo cosa = x6Los símbolos x, y, z (las últimas letras del alfabeto) para representar incógnitas y las primeras para valores conocidos, fue introducido por el libro la Geometrie de Descartes. Parece ser que cuando el libro se estaba componiendo en la imprenta se dieron cuenta que debido a la gran cantidad de ecuaciones que tenía el libro, se quedaban sin letras, por ello el editor le preguntó a Descartes si podía emplear otras letras para las ecuaciones. Descartes le respondió que era indiferente las letras que utilizase en las ecuaciones. El editor eligio la x porque en frances esa letra se utiliza poco.
Sin embargo, no es seguro que esta sea la explicación correcta. Otra explicación es que x se usó como abreviatura de la palabra árabe shei (cosa).
Símbolos de cálculo:
El símbolo Ñ (operador Hamiltoniano) fue introducido por Hamilton en Lectures on Quaternions, y le llamó nabla, porque se asemeja a un antiguo instrumento musical hebreo de ese nombre.
El símbolo ò (para la integral) fue usado por primera vez por Gottfried Wilhelm Leibniz .
Los símbolos dx, dy y dx/dy, para las derivadas, fueron introducidos por Leibniz.
Los símbolos f´(x), f´´(x), etc. para las derivadas, fueron introducidos por Lagrange en 1797 en Théorie des fonctions analytiques.
El símbolo d para la derivada parcial fue usada en 1770 por Antoine-Nicolas Caritat, marques de Condorcet en Memoire sur les Equations aux différence partielles. Jacobi usó este símbolo extensamente, por ello se le suele llamar la delta de Jacobi.
La flecha (® ) de los límites se debe a Godfrey Harold Hardy en A Course of pure Mathematics.
Visita la página http://members.aol.com/jeff570 si estas interesado en este tema.
Antiguamente se utilizaban palabras para referirse a los símbolos, por ejemplo para el signo igual se utilizaba aequales, aequantur, o abrevituras como aeq. El símbolo = aparece por primera vez en The Whetstone of whitte (El aguzador del ingenio) publicada en 1557 por Robert Recorde, que es el primer tratado inglés de álgebra. El autor afirma que eligió ese símbolo porque dos cosas no pueden ser más iguales que dos rectas paralelas. Este símbolo se generalizó hacia finales del siglo XVII; todavía en este siglo Descartes utiliza un signo semejante al símbolo del infinito, probable corrupción de la inicial de la palabra ae qualis (igual en latín).
Los símbolos <, > se deben a Thomas Harriot. Los utilizó en su libro póstumo Artis Analyticae Praxis ad aequationes Algebraicas Resolvendas.
Los símbolos actuales para representar, no igual, no mayor que, no menor que, se deben a Euler.
El símbolo :: fue introducido por William Oughtred en su libro Clavis Mathematicae (1631). Oughtred escribía las proporciones asi: a.b::c.d
La notación actual de las proporciones (a:b::c:d) se debe al astronomo Vincent Wing (1619-1668).
Simbolos de operaciones:
El símbolo x para la multiplicación parece ser original de Oughtred.
El símbolo . para la multiplicación fue utilizado por Thomas Harriot, pero quien lo popularizó fue Leibniz.
El símbolo Ö para la raíz, aparece por primera vez en el primer álgebra publicada en alemán vulgar, en 1525, de Christoff Rudolff.
Símbolos de constantes:
El símbolo p fue usado en 1647 por William Oughtred, para representar la circunferencia de un círculo. William Jones en 1706 en Sypnosis palmariorum mathesios, fue quien primero lo utilizó para la relación entre la longitud de la circunferencia y el diámetro. Sin embargo fue Leonhard Euler quien lo popularizó en 1748 en Introductio in Analysin Infinitorum.
El símbolo e fue usado por Leonhard Euler en el manuscrito Meditatio in Experimenta explosione tormentorum nuper instituta (Meditaciones sobre experimentos hechos recientemente sobre el fuego de un cañón) escrito en 1728.
El símbolo i, para la unidad imaginaria, fue usado por primera vez por Leonhard Euler en 1777 en Institutionum calculi integralis.
El símbolo f para la relacion aurea fue elegido por el matemático americano Mark Barr. La letra fue elegida porque era la primera letra del nombre de Phidias que solia usar la relacion aurea en sus esculturas.
Símbolos de números:
El símbolo 0 (cero) es muy reciente; recuerdese que los romanos no tenían un símbolo para representar el cero.
Parece ser que el cero se utilizaba en la India antes del nacimiento de Jesucristo, pero no hay ninguna evidencia escrita hasta mucho despues, en cualquier caso hay muchas evidencias que indican que el símbolo del cero surgió en la India.
Se discute si el símbolo que utilizaba Ptolomeo (la letra griega ómicron) representaba el cero.
El primer matemático europeo que defendió el uso del cero fue Leonardo de Pisa (más conocido por Fibonacci) en su libor Liber Abaci. Llamó al símbolo zephirum.
Símbolos de variables:
Diofanto usaba una letra griega con acento para representar una cantidad desconocida.
En la Edad Media se utilizaban palabras para representar cantidades desconocidas:
cosa = x
census = x2
cubo = x3
censo di censo = x4
cubo relato cosa = x5
cubo di cubo cosa = x6Los símbolos x, y, z (las últimas letras del alfabeto) para representar incógnitas y las primeras para valores conocidos, fue introducido por el libro la Geometrie de Descartes. Parece ser que cuando el libro se estaba componiendo en la imprenta se dieron cuenta que debido a la gran cantidad de ecuaciones que tenía el libro, se quedaban sin letras, por ello el editor le preguntó a Descartes si podía emplear otras letras para las ecuaciones. Descartes le respondió que era indiferente las letras que utilizase en las ecuaciones. El editor eligio la x porque en frances esa letra se utiliza poco.
Sin embargo, no es seguro que esta sea la explicación correcta. Otra explicación es que x se usó como abreviatura de la palabra árabe shei (cosa).
Símbolos de cálculo:
El símbolo Ñ (operador Hamiltoniano) fue introducido por Hamilton en Lectures on Quaternions, y le llamó nabla, porque se asemeja a un antiguo instrumento musical hebreo de ese nombre.
El símbolo ò (para la integral) fue usado por primera vez por Gottfried Wilhelm Leibniz .
Los símbolos dx, dy y dx/dy, para las derivadas, fueron introducidos por Leibniz.
Los símbolos f´(x), f´´(x), etc. para las derivadas, fueron introducidos por Lagrange en 1797 en Théorie des fonctions analytiques.
El símbolo d para la derivada parcial fue usada en 1770 por Antoine-Nicolas Caritat, marques de Condorcet en Memoire sur les Equations aux différence partielles. Jacobi usó este símbolo extensamente, por ello se le suele llamar la delta de Jacobi.
La flecha (® ) de los límites se debe a Godfrey Harold Hardy en A Course of pure Mathematics.
Visita la página http://members.aol.com/jeff570 si estas interesado en este tema.
Poliedros: Son cuerpos con todas sus caras planas:
Prisma: Es un poliedro cuyas bases son poligonos iguales y las caras paralelogramos.
El segmento común a dos caras se llama arista.
Vértice es el punto de unión de dos aristas.
El prisma es recto si las aristas son perpendiculares a la base.
El prisma es regular si es recto y sus bases son ppligonos regulares.
El volumen de un prisma es el área de la base por la altura (V = A.h)
Paralelepipedo: Es un prisma cuyas pases son paralelogramos.
Piramide: Es un poliedro cuya base es un polígono y las caras son triángulos.
Una piramide es regular si la base es un polígono regular y la altura pasa por el centro.
El volumen de una piramide es 1/3 A.h.
Una piramide cuya es un triangulo se llama tetraedro.
Cuerpos con alguna cara curva:
Cilindro: Es el cuerpo que se genera cuando un segmento de recta se desplaza apoyandose en dos circunferencias iguales y paralelas.
El volumen de un cilindro es el área de la base por la altura (V = A.h)
Cono: Es el cuerpo que se genera cuando un segmento de recta se desplaza apoyandose en una circunferencia y en un punto (situado en un palno distinto a la circunferencia).
El volumen de cono es 1/3 A.h.
Esfera: Es la superficie que tiene la propiedad de que todos sus puntos estan a la misma distancia (radio) de un punto (centro).
El área de la esfera es 4p r2.
El volumen de la esfera es 4/3p r3.
La ecuación de una esfera es: x2 + y2 + z2 = r2
Prisma: Es un poliedro cuyas bases son poligonos iguales y las caras paralelogramos.
El segmento común a dos caras se llama arista.
Vértice es el punto de unión de dos aristas.
El prisma es recto si las aristas son perpendiculares a la base.
El prisma es regular si es recto y sus bases son ppligonos regulares.
El volumen de un prisma es el área de la base por la altura (V = A.h)
Paralelepipedo: Es un prisma cuyas pases son paralelogramos.
Piramide: Es un poliedro cuya base es un polígono y las caras son triángulos.
Una piramide es regular si la base es un polígono regular y la altura pasa por el centro.
El volumen de una piramide es 1/3 A.h.
Una piramide cuya es un triangulo se llama tetraedro.
Cuerpos con alguna cara curva:
Cilindro: Es el cuerpo que se genera cuando un segmento de recta se desplaza apoyandose en dos circunferencias iguales y paralelas.
El volumen de un cilindro es el área de la base por la altura (V = A.h)
Cono: Es el cuerpo que se genera cuando un segmento de recta se desplaza apoyandose en una circunferencia y en un punto (situado en un palno distinto a la circunferencia).
El volumen de cono es 1/3 A.h.
Esfera: Es la superficie que tiene la propiedad de que todos sus puntos estan a la misma distancia (radio) de un punto (centro).
El área de la esfera es 4p r2.
El volumen de la esfera es 4/3p r3.
La ecuación de una esfera es: x2 + y2 + z2 = r2
Elipse: Es una linea cerrada que tiene la propiedad de que la suma de las distancias a dos puntos dados (focos) es constante.
El segmento de recta que une los dos puntos mas alejados se llama eje mayor (=2a).
El segmento de recta que une los dos puntos menos alejados se llama eje menor (=2b).
Centro es el punto de corte de los ejes.
Vértices son los cuatro puntos donde los ejes cortan a la elipse.
Focos son dos puntos, situados en el eje mayor, a igual distancia del centro y que cumplen la condición de que la suma de las distancias desde esos puntos a cualquier punto de la elipse, es constante (=2a).
El área de la superficie encerrada por la elipse es p ab.
La ecuación de una elipse es: x2/a2 + y2/b2 = 1.
El segmento de recta que une los dos puntos mas alejados se llama eje mayor (=2a).
El segmento de recta que une los dos puntos menos alejados se llama eje menor (=2b).
Centro es el punto de corte de los ejes.
Vértices son los cuatro puntos donde los ejes cortan a la elipse.
Focos son dos puntos, situados en el eje mayor, a igual distancia del centro y que cumplen la condición de que la suma de las distancias desde esos puntos a cualquier punto de la elipse, es constante (=2a).
El área de la superficie encerrada por la elipse es p ab.
La ecuación de una elipse es: x2/a2 + y2/b2 = 1.
Circunferencia: Es una linea cerrada que tiene la propiedad de que todos los puntos de esa linea estan a la misma distancia de un punto fijo (centro).
El segmento de recta que va desde el centro hasta la circunferencia se llama radio. El segmento de recta que va desde un punto de la circunferencia a otro pasando por el centro se llama diámetro.
Las circunferencias tienen una propiedad muy notable: Si medimos la longitud de una circunferencia y la dividimos por su diámetro siempre da el mismo número. A ese número le han dado el nombre de p.
La longitud de la circunferencia es 2 pr.
La superficie limitada por la circunferencia se llama círculo. El área del círculo es p r2.
La ecuación de una circunferencia de centro el origen de coordenadas es: x2 + y2 =R2.
El segmento de recta que va desde el centro hasta la circunferencia se llama radio. El segmento de recta que va desde un punto de la circunferencia a otro pasando por el centro se llama diámetro.
Las circunferencias tienen una propiedad muy notable: Si medimos la longitud de una circunferencia y la dividimos por su diámetro siempre da el mismo número. A ese número le han dado el nombre de p.
La longitud de la circunferencia es 2 pr.
La superficie limitada por la circunferencia se llama círculo. El área del círculo es p r2.
La ecuación de una circunferencia de centro el origen de coordenadas es: x2 + y2 =R2.
Cuadrilateros
Cuadrilateros: Son poligonos que tienen cuatro lados.
Paralelogramos: Son cuadrilateros que tienen sus lados paralelos dos a dos. Son paralelogramos el rectángulo, el cuadrado y el rombo.
Trapecio: es un cuadrilatero que tiene dos lados paralelos.
Paralelogramos: Son cuadrilateros que tienen sus lados paralelos dos a dos. Son paralelogramos el rectángulo, el cuadrado y el rombo.
Trapecio: es un cuadrilatero que tiene dos lados paralelos.
Triángulos
Es un poligono que tiene tres lados y tres ángulos.
El punto donde se unen dos lados se llama vértice.
La suma de dos lados de un triángulo siempre es mayor que el tercero.
La suma de los ángulos de un triángulo es 180º.
Es muy frecuente clasificar los triángulos por los lados (equilátero, si tiene los tres lados iguales, isosceles, dos lados iguales y escaleno, ningun lado igual) y por los ángulos (rectángulo si tiene un ángulo de 90º, acutángulo si todos los angulos son menores de 90º y obtusángulo si tiene un ángulo mayor de 90º)
El punto donde se unen dos lados se llama vértice.
La suma de dos lados de un triángulo siempre es mayor que el tercero.
La suma de los ángulos de un triángulo es 180º.
Es muy frecuente clasificar los triángulos por los lados (equilátero, si tiene los tres lados iguales, isosceles, dos lados iguales y escaleno, ningun lado igual) y por los ángulos (rectángulo si tiene un ángulo de 90º, acutángulo si todos los angulos son menores de 90º y obtusángulo si tiene un ángulo mayor de 90º)
Mediana
Es la recta que pasa por un vértice y por el punto medio del lado opuesto. Hay tres medianas y las tres se cortan en un punto que se llama centro de gravedad (o baricentro) del triangulo.
Bisectriz
Es la recta que que divide el ángulo en dos partes iguales. Hay tres bisectrices y se cortan en un punto llamado incentro. Este punto tiene la particularidad de que haciendo centro en él, podemos dibujar una circunferencia interior al triángulo y que es tangente a los tres lados del triangulo.
Mediatriz
Es la recta perpendicular en el punto medio de un segmento. Las mediatrices de los lados de un triángulo se cortan en un punto llamado circuncentro. Haciendo centro en este punto, podemos trazar una circunferencia que pasa por los tres vértices del triángulo.
Altura
Es la recta que pasa por un vértice y es perpendicular al lado opuesto. Hay tres alturas y se cortan en un punto llamado ortocentro.
Es la recta que pasa por un vértice y por el punto medio del lado opuesto. Hay tres medianas y las tres se cortan en un punto que se llama centro de gravedad (o baricentro) del triangulo.
Bisectriz
Es la recta que que divide el ángulo en dos partes iguales. Hay tres bisectrices y se cortan en un punto llamado incentro. Este punto tiene la particularidad de que haciendo centro en él, podemos dibujar una circunferencia interior al triángulo y que es tangente a los tres lados del triangulo.
Mediatriz
Es la recta perpendicular en el punto medio de un segmento. Las mediatrices de los lados de un triángulo se cortan en un punto llamado circuncentro. Haciendo centro en este punto, podemos trazar una circunferencia que pasa por los tres vértices del triángulo.
Altura
Es la recta que pasa por un vértice y es perpendicular al lado opuesto. Hay tres alturas y se cortan en un punto llamado ortocentro.
El triángulo más famoso es es triángulo rectángulo. El lado mayor de un triángulo rectángulo se llama hipotenusa y los pequeños, catetos. Este triángulo tiene una propiedad muy importante: Si construimos unos cuadrados en sus lados, la suma del área de los cuadrados construidos en los catetos es igual al área del cuadrado construido en la hipotenusa (escrito de forma matemática: a2 + b2 =c2).
Superficie de un triángulo:
La fórmula que todos sabemos de la superficie de un triángulo es S = (b.h)/2
Hay otra fórmula menos conocida, la fómula de Herón:
siendo p = (a + b + c)/2
Superficie de un triángulo:
La fórmula que todos sabemos de la superficie de un triángulo es S = (b.h)/2
Hay otra fórmula menos conocida, la fómula de Herón:
siendo p = (a + b + c)/2
miércoles, enero 17, 2007
martes, enero 16, 2007
A Pedro, el herrero, le trajeron cinco trozos de cadena de tres eslabones cada uno, para que los transformara en una cadena continua.
Pedro meditó un rato y decidió que tendría que abrir cuatro eslabones y volver a forjarlos, pues tendría que abrir cuatro anillos y luego cerrarlos uniendo los trozos de cadena.
¿Pedro podría abrir y enlazar un número menor de anillos?
Pedro podría realizar el trabajo, soltando los tres eslabones de un trozo de cadena, y usarlos individualmente, uniendo los extremos de los cuatro trozos restantes.
Pedro meditó un rato y decidió que tendría que abrir cuatro eslabones y volver a forjarlos, pues tendría que abrir cuatro anillos y luego cerrarlos uniendo los trozos de cadena.
¿Pedro podría abrir y enlazar un número menor de anillos?
Pedro podría realizar el trabajo, soltando los tres eslabones de un trozo de cadena, y usarlos individualmente, uniendo los extremos de los cuatro trozos restantes.
miércoles, enero 10, 2007
viernes, enero 05, 2007
CRITERIOS DE DIVISIBILIDAD............
http://sauce.pntic.mec.es/jdiego/glosario/divisibilidad.swf
Criterios de divisibilidad
Los criterios de divisibilidad son reglas que sirven para saber si un número es divisible por otro sin necesidad de realizar la división. Aunque pueden buscarse criterios para todos los números, sólo expondremos los más comunes:
Criterio de divisibilidad por 2 Un número es divisible por 2 si acaba en 0 o cifra par.
Ejemplos: Números divisibles por 2: 36,94,521342,40,...
Criterio de divisibilidad por 3 Un número es divisible por 3 si la suma de sus cifras es múltiplo de 3.
Ejemplos: Números divisibles por 3: 36,2142,42,...
Criterio de divisibilidad por 5 Un número es divisible por 5 si la última de sus cifras es 5 o es 0.
Ejemplos: Números divisibles por 5: 35,2145,40,...
Criterio de divisibilidad por 9 Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.
Ejemplos: Números divisibles por 9: 495,945,53640,...
Criterio de divisibilidad por 11 Debemos hacer lo siguiente: Sumamos las cifras que ocupan lugares pares, sumamos las cifras que ocupan lugares impares. A la suma mayor le restamos la suma menor, si la diferencia es 0 o múltiplo de 11, entonces el número es múltiplo de 11.
Ejemplos: Múltiplos de 11: 2343649,9889,18161902,...
Criterios de divisibilidad
Los criterios de divisibilidad son reglas que sirven para saber si un número es divisible por otro sin necesidad de realizar la división. Aunque pueden buscarse criterios para todos los números, sólo expondremos los más comunes:
Criterio de divisibilidad por 2 Un número es divisible por 2 si acaba en 0 o cifra par.
Ejemplos: Números divisibles por 2: 36,94,521342,40,...
Criterio de divisibilidad por 3 Un número es divisible por 3 si la suma de sus cifras es múltiplo de 3.
Ejemplos: Números divisibles por 3: 36,2142,42,...
Criterio de divisibilidad por 5 Un número es divisible por 5 si la última de sus cifras es 5 o es 0.
Ejemplos: Números divisibles por 5: 35,2145,40,...
Criterio de divisibilidad por 9 Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.
Ejemplos: Números divisibles por 9: 495,945,53640,...
Criterio de divisibilidad por 11 Debemos hacer lo siguiente: Sumamos las cifras que ocupan lugares pares, sumamos las cifras que ocupan lugares impares. A la suma mayor le restamos la suma menor, si la diferencia es 0 o múltiplo de 11, entonces el número es múltiplo de 11.
Ejemplos: Múltiplos de 11: 2343649,9889,18161902,...
miércoles, enero 03, 2007
Expresiones Algebraicas
Las expresiones algebraicas se clasifican según su número de términos.
monomio = un solo término.
binomio = suma o resta de dos mono
trinomio = suma o resta de tres monomios.
polinomio = suma o resta de cualquier número de monomios.
monomio = un solo término.
binomio = suma o resta de dos mono
trinomio = suma o resta de tres monomios.
polinomio = suma o resta de cualquier número de monomios.
Reglas de los Signos:
En suma de números con signos iguales, se suman los números y el resultado lleva el mismo signo. Si los números tienen signos diferentes, se restan y el resultado lleva el signo del mayor.
Ejemplo:
5 + 8 = 13
5 + -8 = -3
En resta de signos iguales el resultado lleva el signo del mayor. Si se restan signos diferentes, se suman los números y el resultado lleva el signo del mayor.
Ejemplo:
5 - 8 = -3
5 - (-8) = 13
En multiplicación y división de números con signos iguales el resultado es positivo. Si los números son signos opuestos, el resultado es negativo.
Ejemplo:
5 x 8 = 40
5 x -8 = -40
Ejemplo:
5 + 8 = 13
5 + -8 = -3
En resta de signos iguales el resultado lleva el signo del mayor. Si se restan signos diferentes, se suman los números y el resultado lleva el signo del mayor.
Ejemplo:
5 - 8 = -3
5 - (-8) = 13
En multiplicación y división de números con signos iguales el resultado es positivo. Si los números son signos opuestos, el resultado es negativo.
Ejemplo:
5 x 8 = 40
5 x -8 = -40
Orden de Operaciones
Reglas Importantes para Resolver Operaciones Aritméticas:
Primero resolver todo lo que esté dentro de simbolos de agrupación.
Evaluar las expresiones exponenciales.
Hacer todas las multiplicaciones y divisiones en orden de izquierda a derecha.
Hacer todas las sumas y restas en orden de izquierda a derecha.
NÚMEROS REALES
Los números que se utilizan en el álgebra son los números reales. Hay un número real en cada punto de la recta numérica. Los números reales se dividen en números racionales, números irracionales y numeros enteros los cuales a su vez se dividen en números negativos, números positivos y cero (0) .Podemos verlo en esta tabla:
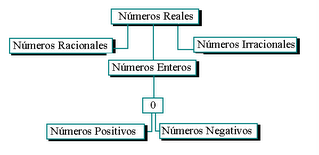
Un número real es racional si se puede representar como cociente a/b, donde a sea un entero y b sea un entero no igual a cero. Los números racionales pueden escribirse en forma decimal. Existen dos maneras:
* decimales terminales
* decimales que se repiten infinitamente
Los números reales que no pueden ser expresados en la forma a/b, donde a y b son enteros se llaman números irracionales. Los números irracionales no tienen decimales terminales ni decimales que se repiten infinitamente

Un número real es racional si se puede representar como cociente a/b, donde a sea un entero y b sea un entero no igual a cero. Los números racionales pueden escribirse en forma decimal. Existen dos maneras:
* decimales terminales
* decimales que se repiten infinitamente
Los números reales que no pueden ser expresados en la forma a/b, donde a y b son enteros se llaman números irracionales. Los números irracionales no tienen decimales terminales ni decimales que se repiten infinitamente
lunes, enero 01, 2007
Suscribirse a:
Comentarios (Atom)





