domingo, diciembre 31, 2006
ÁRBOL DE NAVIDAD....
Un Mini acertijo para pensar apenas concluyan los brindis:
¿Cuántos cuadrados pueden contar en el arbolito navideño del dibujo?
Criptosuma
Recuerden que a letra distinta va un numero distinto y que una palabra no puede comenzar con 0. Resolver sabiendo que SEIS es divisible por 6.
SEIS + DE + ENERO = REYES
SEIS + DE + ENERO = REYES; 4104 + 81 + 17129 = 21314
SEIS + DE + ENERO = REYES
SEIS + DE + ENERO = REYES; 4104 + 81 + 17129 = 21314
Silábicos
Se trata de encontrar palabras que se dividan en 4 sílabas de 1,2,3y4 letras en todos los ordenes posibles.
Existirán para las 24 combinaciones?
Ejemplo: RE-CRE-A-CION = 2-3-1-4.
1234) A NI MAS TEIS
1243) I NI CIAR NOS
1324) A CEP TA CION
1342) A RRE PIEN TO
1423) A TRAC TI VOS
1432) O RIEN TAR LO
2134) RE E LEC CION
2143) ZO O PLAS TOS
2314) RE CRE A CION
2341)
2413)
2431) TE TRAR QUI A
3124) PRE O CU PAIS
3142) CLO A QUIS TA
3214) DES VI A CION
3241)
3412)
3421) COM PREN DI A
4123) TRES A ÑE JOS
4132) TRES A BUE LO
4213) FRAN JE A RAIS
4231) TRAS CU RRI A
4312) FRAN QUE A DO
4321) FIAM BRE RI A
Existirán para las 24 combinaciones?
Ejemplo: RE-CRE-A-CION = 2-3-1-4.
1234) A NI MAS TEIS
1243) I NI CIAR NOS
1324) A CEP TA CION
1342) A RRE PIEN TO
1423) A TRAC TI VOS
1432) O RIEN TAR LO
2134) RE E LEC CION
2143) ZO O PLAS TOS
2314) RE CRE A CION
2341)
2413)
2431) TE TRAR QUI A
3124) PRE O CU PAIS
3142) CLO A QUIS TA
3214) DES VI A CION
3241)
3412)
3421) COM PREN DI A
4123) TRES A ÑE JOS
4132) TRES A BUE LO
4213) FRAN JE A RAIS
4231) TRAS CU RRI A
4312) FRAN QUE A DO
4321) FIAM BRE RI A
EJERCICIOS.....MUY BUENO
Ejercicios on-line de sumar, restar, multiplicar, con fracciones. Conversión de unidades, Teoremas. Fórmulas geométricas.
http://www.salonhogar.com/matemat/index.htm
http://www.salonhogar.com/matemat/index.htm
APLUSMATH...
Ejercicios y juegos de cálculo mental con las cuatro operaciones, con fracciones y números decimales. Ejercicios para imprimir y comprobar posteriormente los resultados. (En inglés)
http://www.aplusmath.com/
http://www.aplusmath.com/
CURRICULO DE MATEMÁTICAS
Contenidos mínimos
BOE del 16/1/2001
ESO: Páginas de 1810 a 1858
Matemáticas: Páginas de 1842 a 1845
Horarios: 1850
Bachilleratos: Páginas 1858 a 1922
Tipos de bachillerato: 1860
Matemáticas:
Bachillerato de Ciencias de la Naturaleza y de la Salud: Páginas de 1842 a 1845
Bachillerato de Humanidades y Ciencias Sociales: Páginas de 1909 a 1910
Bachillerato de Tecnología: Páginas de 1916 a 1918 (Es el mismo que el del Bachillerato de Ciencias de la Naturaleza y de la Salud)
Desarrollo del currículo
BOE del 7/9/2001
ESO: Páginas de 33733 a 33795
Matemáticas: Páginas de 33772 a 33777
Bachilleratos: Páginas 33795 a 33880
Matemáticas:
Bachillerato de Ciencias de la Naturaleza y de la Salud: Páginas de 33839 a 33842
Bachillerato de Humanidades y Ciencias Sociales: Páginas de 33858 a 33860
Bachillerato de Tecnología: Páginas de 33867 a 33870 (Es el mismo que el del Bachillerato de Ciencias de la Naturaleza y de la Salud)
BOE del 16/1/2001
ESO: Páginas de 1810 a 1858
Matemáticas: Páginas de 1842 a 1845
Horarios: 1850
Bachilleratos: Páginas 1858 a 1922
Tipos de bachillerato: 1860
Matemáticas:
Bachillerato de Ciencias de la Naturaleza y de la Salud: Páginas de 1842 a 1845
Bachillerato de Humanidades y Ciencias Sociales: Páginas de 1909 a 1910
Bachillerato de Tecnología: Páginas de 1916 a 1918 (Es el mismo que el del Bachillerato de Ciencias de la Naturaleza y de la Salud)
Desarrollo del currículo
BOE del 7/9/2001
ESO: Páginas de 33733 a 33795
Matemáticas: Páginas de 33772 a 33777
Bachilleratos: Páginas 33795 a 33880
Matemáticas:
Bachillerato de Ciencias de la Naturaleza y de la Salud: Páginas de 33839 a 33842
Bachillerato de Humanidades y Ciencias Sociales: Páginas de 33858 a 33860
Bachillerato de Tecnología: Páginas de 33867 a 33870 (Es el mismo que el del Bachillerato de Ciencias de la Naturaleza y de la Salud)
Reparto de 11 casas
Trata de adivinar que hay de extraño en el siguiente relato:
Un famoso y rico constructor poseía 11 casas en la pequeña ciudad donde vivía, además de una gran mansión donde residía junto a su esposa y sus tres hijos. Cuando murió dejó un testamento en el que pedía que la mansión fuese para su esposa y que las 11 casas fuesen repartidas entre sus tres hijos de la siguiente forma:
"La mitad de ellas debían ser para el hijo mayor; la cuarta parte, para el mediano, y una sexta parte de ellas para el benjamín."
Los hijos estaban bastante sorprendidos
¿Cómo dividir 11 casas en dos partes iguales?, ¿o en cuatro?, ¿y en seis?
Mientras los hijos discutían qué hacer, la madre se acercó y les propuso que contasen también con la mansión para hacer el reparto.
Entonces el hijo mayor dijo que él se quedaría con seis casas, la mitad de 12, el mediano con tres, la cuarta parte de 12, y el pequeño con 2, la sexta parte de 12; con lo cual habían cumplido con lo propuesto en el testamento.
Después del reparto, la madre se dio cuenta que se habían repartido las 11 casas ( 6 + 3 + 2 ) y que podía seguir quedándose con la mansión.
Si descubres lo extraño de este relato mándanos un mensaje por correo electrónico
Un famoso y rico constructor poseía 11 casas en la pequeña ciudad donde vivía, además de una gran mansión donde residía junto a su esposa y sus tres hijos. Cuando murió dejó un testamento en el que pedía que la mansión fuese para su esposa y que las 11 casas fuesen repartidas entre sus tres hijos de la siguiente forma:
"La mitad de ellas debían ser para el hijo mayor; la cuarta parte, para el mediano, y una sexta parte de ellas para el benjamín."
Los hijos estaban bastante sorprendidos
¿Cómo dividir 11 casas en dos partes iguales?, ¿o en cuatro?, ¿y en seis?
Mientras los hijos discutían qué hacer, la madre se acercó y les propuso que contasen también con la mansión para hacer el reparto.
Entonces el hijo mayor dijo que él se quedaría con seis casas, la mitad de 12, el mediano con tres, la cuarta parte de 12, y el pequeño con 2, la sexta parte de 12; con lo cual habían cumplido con lo propuesto en el testamento.
Después del reparto, la madre se dio cuenta que se habían repartido las 11 casas ( 6 + 3 + 2 ) y que podía seguir quedándose con la mansión.
Si descubres lo extraño de este relato mándanos un mensaje por correo electrónico
MENTAL
Calcula, mentalmente, el M.C.D. y el m.c.m. de los siguientes pares de números.
a) M.C.D.(4, 6) =
m.c.m.(4, 6) =
b) M.C.D.(8, 12) =
m.c.m.(8, 12) =
c) M.C.D.(8, 5) =
m.c.m.(8, 5) =
a) M.C.D.(4, 6) =
m.c.m.(4, 6) =
b) M.C.D.(8, 12) =
m.c.m.(8, 12) =
c) M.C.D.(8, 5) =
m.c.m.(8, 5) =
ABSCISA
Medida tomada sobre el eje horizontal en el sistema de coordenadas cartesiano.Es el primero de las dos coordenadas que hacen referencia a un punto.Así, el punto de coordenadas (3, 2) tiene como abscisa el número 3.
sábado, diciembre 30, 2006
ALGEBRA ....IDENTIDADES
Clausura de la Adición (la Suma)
El sumando (o la diferencia) de dos números reales es igual a un númemero real.
Identidad Aditiva
a + 0 = a
Inverso Aditivo
a + (-a) = 0
Asociatividad de la Adición (la Suma)
(a + b) + c = a + (b + c)
Conmutatividad de la Adición (la Suma)
a + b = b + a
La Definición de la Substracción
a - b = a + (-b)
Clausura de la Multiplicación (el Producto)
El producto (o el cociente si el denominador 0) de dos números reales es igual a un número real.
Identidad Multiplicativa
a * 1 = a
Inverso Multiplicativo
a * (1/a) = 1 (a 0)
Multiplicación por 0
a * 0 = 0
Asociatividad de la Multiplicación (el Producto)
(a * b) * c = a * (b * c)
Conmutatividad de la Multiplicación (el Producto)
a * b = b * a
Ley Distributiva
a(b + c) = ab + ac
La Definición de División
a / b = a(1/b)
El sumando (o la diferencia) de dos números reales es igual a un númemero real.
Identidad Aditiva
a + 0 = a
Inverso Aditivo
a + (-a) = 0
Asociatividad de la Adición (la Suma)
(a + b) + c = a + (b + c)
Conmutatividad de la Adición (la Suma)
a + b = b + a
La Definición de la Substracción
a - b = a + (-b)
Clausura de la Multiplicación (el Producto)
El producto (o el cociente si el denominador 0) de dos números reales es igual a un número real.
Identidad Multiplicativa
a * 1 = a
Inverso Multiplicativo
a * (1/a) = 1 (a 0)
Multiplicación por 0
a * 0 = 0
Asociatividad de la Multiplicación (el Producto)
(a * b) * c = a * (b * c)
Conmutatividad de la Multiplicación (el Producto)
a * b = b * a
Ley Distributiva
a(b + c) = ab + ac
La Definición de División
a / b = a(1/b)
viernes, diciembre 29, 2006
jueves, diciembre 28, 2006
lunes, diciembre 25, 2006
Eres el piloto de una avioneta que es capaz de viajar a una velocidad de 300 km/h sin viento.Tienes combustible para 4 horas de vuelo. Despegas del aeropuerto y en el viaje de ida tienes un viento a favor de 50 km/h, lo que eleva tu velocidad hasta 350 km/h. De repente te das cuenta de que en el viaje de vuelta tendrás el viento en contra y volarás a 250 km/h. Puedes ayudarte de una gráfica que muestre cómo varía la distancia al aeropuerto en función del tiempo para calcular la máxima distancia a la que puedes llegar.
Disponemos de tres dados en los que hemos pintado las caras así:
Primer dado: 1 1 2 2 3 3 Segundo 1 1 1 2 2 2 Tercero 0 0 1 1 2 2
Encuentra las siguientes probabilidades: a) que los tres dados den un número par b) que los tres tengan el mismo número c) que la suma de los tres dados sea par
Marca 7 puntos no alineados en el plano. ¿Cuántos triángulos distintos puedes obtener uniendo 3 de esos puntos?, ¿cuántos cuadriláteros uniendo 4 puntos?
Hemos rellenado una quiniela múltiple de 14 resultados marcando 3 triples y 4 dobles. ¿A cuántas apuestas simples equivale?
¿Cuántos números hay entre el 3000 y el 7500 que estén formados exclusivamente por cifras impares?
Un entrenador de baloncesto dispone de 3 bases, 4 aleros y 3 pivots. a) ¿Cuántos equipos distintos formados por un base, dos aleros y dos pivots puede formar, respetando la especialidad de cada jugador? b) ¿Y si no respetara la especialidad de los jugadores, es decir que todos pueden jugar en cualquier puesto?
Disponemos de tres dados en los que hemos pintado las caras así:
Primer dado: 1 1 2 2 3 3 Segundo 1 1 1 2 2 2 Tercero 0 0 1 1 2 2
Encuentra las siguientes probabilidades: a) que los tres dados den un número par b) que los tres tengan el mismo número c) que la suma de los tres dados sea par
Marca 7 puntos no alineados en el plano. ¿Cuántos triángulos distintos puedes obtener uniendo 3 de esos puntos?, ¿cuántos cuadriláteros uniendo 4 puntos?
Hemos rellenado una quiniela múltiple de 14 resultados marcando 3 triples y 4 dobles. ¿A cuántas apuestas simples equivale?
¿Cuántos números hay entre el 3000 y el 7500 que estén formados exclusivamente por cifras impares?
Un entrenador de baloncesto dispone de 3 bases, 4 aleros y 3 pivots. a) ¿Cuántos equipos distintos formados por un base, dos aleros y dos pivots puede formar, respetando la especialidad de cada jugador? b) ¿Y si no respetara la especialidad de los jugadores, es decir que todos pueden jugar en cualquier puesto?
NIVEL 3
1. El problema de Newton
En un campo la hierba crece en todas partes con igual rapidez y espesura. Sa sabe que 70 vacas se la comerían en 24 días y 30 vacas en 60 días. ¿Cuántas vacas serían necesarias para comerse toda la hierba en 96 días?
2. Una brigada está formada por 6 armadores y un carpintero. Cada armador gana 20.000 ptas y el carpintero 3.000 ptas más que el salario medio de los miembros de la brigada incluído el mismo. ¿Cuánto ganaba el carpintero?
3. Un coche va por una carrtera a velocidad constante. En un momento dado pasa por delante de un poste kilométrico que tiene un número de dos cifras. Al cabo de una hora pasa por delante de otro poste que curiosamente tiene las mismas dos cifras pero en oden inverso. Su sorpresa es enorme cuando al acbo de otra hora pasa por otro poste que lleva las mismas cifras separadas por un cero. ¿A qué velocidad va el coche?
En un campo la hierba crece en todas partes con igual rapidez y espesura. Sa sabe que 70 vacas se la comerían en 24 días y 30 vacas en 60 días. ¿Cuántas vacas serían necesarias para comerse toda la hierba en 96 días?
2. Una brigada está formada por 6 armadores y un carpintero. Cada armador gana 20.000 ptas y el carpintero 3.000 ptas más que el salario medio de los miembros de la brigada incluído el mismo. ¿Cuánto ganaba el carpintero?
3. Un coche va por una carrtera a velocidad constante. En un momento dado pasa por delante de un poste kilométrico que tiene un número de dos cifras. Al cabo de una hora pasa por delante de otro poste que curiosamente tiene las mismas dos cifras pero en oden inverso. Su sorpresa es enorme cuando al acbo de otra hora pasa por otro poste que lleva las mismas cifras separadas por un cero. ¿A qué velocidad va el coche?
NIVEL 2
1. Un excursionista sale de su casa a las 4 de la tarde para subir a una montaña. Hasta la base de la montaña el terreno es llano y avanza a 4 km/h, subiendo va a 3 km/h y bajando a 6 km/h. Si regresa a las 10 de la noche, ¿cuántos kms ha recorrido en total?
2. ¿Cuántas veces a lo largo de un día las agujas de un reloj forman un ángulo recto?
3. Tres cervezas, 7 refrescos y una ración de calamares cuestan 2800 pts; 4 cervezas, 10 refrescos y una ración cuestan 3400 pts. ¿Cuánto habrá que pagar por una cerveza, un refresco y una ración?
2. ¿Cuántas veces a lo largo de un día las agujas de un reloj forman un ángulo recto?
3. Tres cervezas, 7 refrescos y una ración de calamares cuestan 2800 pts; 4 cervezas, 10 refrescos y una ración cuestan 3400 pts. ¿Cuánto habrá que pagar por una cerveza, un refresco y una ración?
NIVEL 1
1. En la película "La jungla de cristal 2", el malo propone a McCane y a su amigo un problema. Para desactivar una bomba tienen que colocar sobre una maleta una garrafa con 4 litros de agua, pero sólo disponen de una garrafa de 5 litros y otra de 3 litros, ¿cómo lo resuelven?
2. Tres amigos tienen 21 botes de coca-cola, 7 de ellos están llenos, 7 vacíos y 7 llenos hasta la mitad exactamente. ¿Cómo deben repartirse los botes para que los tres se lleven el mismo número de botes y la misma cantidad de coca-cola? ( No se puede trasvasar de un bote a otro)
3. ¿Cómo te las ingeniarías para cortar en 8 trozos iguales un disco de papel, dando sólo tres cortes rectos?
2. Tres amigos tienen 21 botes de coca-cola, 7 de ellos están llenos, 7 vacíos y 7 llenos hasta la mitad exactamente. ¿Cómo deben repartirse los botes para que los tres se lleven el mismo número de botes y la misma cantidad de coca-cola? ( No se puede trasvasar de un bote a otro)
3. ¿Cómo te las ingeniarías para cortar en 8 trozos iguales un disco de papel, dando sólo tres cortes rectos?
La edad de Alfredo
Alfredo, ¿sabes que yo tengo cuatro veces la edad que tú tenías cuando yo tenía la edad que tienes tú ahora? ¿Sabes también que cuando tú tengas la edad que yo tengo ahora, tendremos entre los dos 114 años?
¿Qué edad tiene Alfredo? y ¿yo?
Sugerencia: lee con atención, piensa en la diferencia de edad entre ambos y en que los años pasan para los dos igual. Utiliza ecuaciones si te hace falta.
¿Qué edad tiene Alfredo? y ¿yo?
Sugerencia: lee con atención, piensa en la diferencia de edad entre ambos y en que los años pasan para los dos igual. Utiliza ecuaciones si te hace falta.
La cabra pastando
Una cabra está atada con una cuerda en el borde externo de un corral circular de 24 m de perímetro. La longitud de la cuerda es la mitad del perímetro del corral. ¿qué superficie de cuerda puede alcanzar la cabra?
Este problema es en apariencia sencillo, sin embargo no es tan simple y, para resolverlo vamos a tener que recurrir a algunas estrategias de resolución de problemas.
Para abordarlo es conveniente que:
a) dibujes un diagrama de la situación. No es tan fácil.
b) inténtalo utilizando un tubo cilíndrico y un hilo.
La superficie dibujada no se parece a ninguna de las formas planas cuya área conoces.
ESTRATEGIA: Imagínate un problema parecido pero más sencillo Cambia el corral circular por uno cuadrado del mismo perímetro. Ahora el problema es bastante más sencillo. Dibuja un diagrama de la situación actual. Observa que las regiones que se forman son sectores circulares cuyos radios y amplitudes respectivas puedes deducir facílmente. Cambia el cuadrado por un octógono y repite el proceso
Este problema es en apariencia sencillo, sin embargo no es tan simple y, para resolverlo vamos a tener que recurrir a algunas estrategias de resolución de problemas.
Para abordarlo es conveniente que:
a) dibujes un diagrama de la situación. No es tan fácil.
b) inténtalo utilizando un tubo cilíndrico y un hilo.
La superficie dibujada no se parece a ninguna de las formas planas cuya área conoces.
ESTRATEGIA: Imagínate un problema parecido pero más sencillo Cambia el corral circular por uno cuadrado del mismo perímetro. Ahora el problema es bastante más sencillo. Dibuja un diagrama de la situación actual. Observa que las regiones que se forman son sectores circulares cuyos radios y amplitudes respectivas puedes deducir facílmente. Cambia el cuadrado por un octógono y repite el proceso
6 OPERACIONES
DESCRIPCIÓN
En un tablero de 4X4 casillas se escriben 16 números enteros de 2 cifras.
Por ejemplo
8
35
16
6
15
14
20
11
9
40
12
29
18
35
50
24
El objetivo del juego consiste en obtener los números que aparecen en el tablero realizando dos operaciones con los puntos que se obtengan al lanzar tres dados. Por ejemplo, si han salido en los dados 3 , 3 , 5 puede hacer 3 · (3 + 5) = 24
En este caso tacharía del tablero el número 24 de la esquina inferior derecha
Reglas del juego:
Número de jugadores (2 o 3)
1. Se echa a suertes para ver que jugador comienza.
2. Cada jugador, por orden, lanza los tres dados ( o un dado tres veces ) y obtiene tres números.
3. Con esos números realiza dos operaciones aritméticas ( -, +, · . ÷ ) o elevar un número a otro, o extraer raíces, en las que índice y radicando son dos de los tres números obtenidos pudiendo repetir operación, apuntando en un papel las operaciones realizadas para que las vea el contrario y tacha el número de la tabla obtenido.
4. Si un jugador, con los números obtenidos no puede tachar ninguno de los números libres del tablero, pasa el turno al siguiente jugador.
5. Si un jugador no ha obtenido ningún número de la tabla por no haber encontrado las operaciones convenientes, tacha el número el primer jugador que descubra la combinación adecuada
6. La partida termina cuando todos los números de la tabla estén tachados
7. Gana el jugador que ha tachado más números.
En un tablero de 4X4 casillas se escriben 16 números enteros de 2 cifras.
Por ejemplo
8
35
16
6
15
14
20
11
9
40
12
29
18
35
50
24
El objetivo del juego consiste en obtener los números que aparecen en el tablero realizando dos operaciones con los puntos que se obtengan al lanzar tres dados. Por ejemplo, si han salido en los dados 3 , 3 , 5 puede hacer 3 · (3 + 5) = 24
En este caso tacharía del tablero el número 24 de la esquina inferior derecha
Reglas del juego:
Número de jugadores (2 o 3)
1. Se echa a suertes para ver que jugador comienza.
2. Cada jugador, por orden, lanza los tres dados ( o un dado tres veces ) y obtiene tres números.
3. Con esos números realiza dos operaciones aritméticas ( -, +, · . ÷ ) o elevar un número a otro, o extraer raíces, en las que índice y radicando son dos de los tres números obtenidos pudiendo repetir operación, apuntando en un papel las operaciones realizadas para que las vea el contrario y tacha el número de la tabla obtenido.
4. Si un jugador, con los números obtenidos no puede tachar ninguno de los números libres del tablero, pasa el turno al siguiente jugador.
5. Si un jugador no ha obtenido ningún número de la tabla por no haber encontrado las operaciones convenientes, tacha el número el primer jugador que descubra la combinación adecuada
6. La partida termina cuando todos los números de la tabla estén tachados
7. Gana el jugador que ha tachado más números.
JUEGO DEL 100
JUEGO del 100 ( 4 jugadores, 2 equipos de 2 jugadores )
Cada equipo alternativamente lanza un dado 4 veces y anota los resultados.
Cada equipo tacha todos los números del tablero que haya podido obtener enlazando los números obtenidos mediante 3 operaciones ( se puede utilizar +, -, · , ÷ )
Por ejemplo, si han salido 3, 3, 2, 5 se pueden tachar los siguientes números
(3 · 3) + (2 · 5) = 19
(3 + 3 + 2) · 5 = 40
(3 · 5) - (3 · 2) = 9
(3 · 2 · 5) : 3 = 10
(5 - 2) · 3 · 3 = 27
Gana el equipo que ha tachado más números.
jueves, diciembre 21, 2006
ENLACES MATÉMATICOS
http://www.ieslosviveros.com/matematicas/matematicas.htm Página web del Seminario de Matemáticas del IES Los Viveros de Sevilla.
Refuerza y amplía tus matemáticas es un conjunto de páginas interactivas de Matemáticas, Aritmética, Álgebra y Problemas referidos a las citadas disciplinas, que se autogeneran y autocorrigen cada vez que se seleccionan, listas para ser utilizadas desde los navegadores más conocidos, Mozilla y Explorer, tanto en Guadalinex como en Windows, orientada principalmente al Refuerzo del Área de Matemáticas en el Primer Ciclo de la E.S.O. Lo que no excluye que sirva también como actividades para el Refuerzo y Ampliación tanto en Primaria como en Secundaria.
Materiales para construir la geometría (Primaria) Muy bueno.
http://www.amejor.com/mates/ Problemas matemáticos con "gancho" para primeros cursos de la ESO. Clasificados por ámbitos de contenido, con indicación de su grado de dificultas y las soluciones razonadas.
http://platea.pntic.mec.es/~aperez4/ Completísima página de Antonio Pérez Sanz del I.E.S. Salvador Dalí de Madrid. En ella encontrarás juegos, problemas, curiosidades, experiencias y materiales de aula, numerosos enlaces de interés...
Thales Página de la Sociedad andaluza de educación matemática. Se puede encontrar una amplia variedad de recursos didácticos.
Real Sociedad Matemática Web de la Real Sociedad Matemática Española. Publicaciones, convocatorias, debates, etc.
El Proyecto Descartes está desarrollado en el Centro Nacional de Información y Comunicación Educativa (CNICE) del Ministerio de Educación, Cultura y Deporte, para el uso de los profesores de Matemáticas en sus aulas. Se han desarrollado más de 100 Unidades Didácticas de Secundaria, y se pueden utilizar, no sólo en la web, sino que pueden descargarse los archivos a un ordenador local con suma facilidad.
Es una herramienta interactiva que permite al alumno mover puntos, cambiar parámetros, dibujar, y en definitiva actuar sobre una escena que puede presentar gráficas, puntos, figuras geométricas, textos, etc. directamente en una página web.
De mates ¿na? Elaborada por alumnos de 4º de ESO del instituto "SIERRA MINERA" de La Unión, Murcia.
Tablas Matemáticas de David Manura Página dedicada a las matemáticas, que incluye diversas secciones: Matemáticas generales, álgebra, geometría, trigonometría, cálculo, estadística, etc.... pueden ser descargas para verlas deconectado en un fichero .zip.
Las matemáticas de Mario teoría, problemas resueltos, biografías, lecturas recomendadas, etc.
http://www.linuxforkids.org/edu_math_sp.html Dirección con bastante software matemático para alumnos ACNEE que funcionan en Linux.
http://www.matematicas.net El paraíso de las matemáticas, imprescindible.
http://webs.uolsinectis.com.ar/acoda/apuntes.html Apuntes básicos de Matemáticas organizados por lecciones.
Portal chileno donde encontraras numerosos recursos y enlaces de interés.
OKmath, en este portal encontrarás cientos de problemas y ejercicios de matemáticas resueltos paso a paso.
http://nti.educa.rcanaria.es/matematicas/ página recopilada por Manuel de Armas Cruz. Colección de enlaces sobre diferentes aspectos de las matemáticas (historia, juegos, olimpiadas, software,...).
http://www.xtec.es/%7Ejcorder1/index.htm Matemáticas básicas de Primaria y ESO.
http://www.elosiodelosantos.com Este portal educativo cuenta con software educativo interactivo en línea y gratuito, con páginas para la resolución de problemas de matemáticas y con más de 12000 ejercicios resueltos.El acceso a los recursos es libre, gratuito y sin contraseñas
http://platea.pntic.mec.es/~jescuder/ Jesús ESCUDERO Profesor del I. E. S. Fray Luis de León de Salamanca) Acertijos, problemas, curiosidades...
2piMath de Jesus Plaza. Resúmenes, ejercicios, problemas, utilidades, software y enlaces.
Mis mates de Mª Dolores Rodríguez. Actividades para el aula, artículos, referencias de libros, etc.
Olimpiadas matemáticas . Todo sobre las Olimpiadas Matemáticas: qué son, convocatorias, información a los profesores, problemas de las últimas olimpiadas, material para la preparación,...
Gacetilla matemática. Contiene problemas, libros, anécdotas, información sobre los grandes matemáticos de la historia y enlaces con las mejores webs sobre la materia
http://platea.pntic.mec.es/~mzapata/matemat.htm de Miguel Zapata. Ejercicios, enlaces de interés...
http://roble.pntic.mec.es/~jbrihueg/ En esta página podrás encontrar actividades de clase y problemas para la Educación Secundaria(algunos de las Pruebas de acceso a la Universidad) organizados por temas y niveles.
Juegos y problemas de ingenio del club Mensa. Colección de los juegos de ingenio que se publican en las revistas y páginas web de Mensa.
http://www.ecomur.com Ecomur es un portal de economía y enseñanza dirigido a estudiantes y profesores de bachillerato, con recursos didácticos de las asignaturas de economía y enlaces educativos y económicos de interés. www.deberesmatematicas.com Herramientas didácticas específicas para la enseñanza y el aprendizaje de las matemáticas de la E.S.O. Ejercicios, problemas, exámenes, temarios, todos resueltos y explicados paso a paso. La suscripción para profesores es GRATUITA.Ejercicios de Matemáticas. Esta web ofrece una parte teórica y actividades resueltas que van a facilitar el aprendizaje. Cada uno de los apartados presenta unas herramientas para su desarrollo y ejercicios de repaso resueltos paso a paso, 3º- 4º E.S.O. http://www.ecobachillerato.com (Economía de Bachillerato) de Tomas Guajardo Cuervo. Multitud de materiales de interés para profesores y alumnos. Curiosidades Matemáticas.
Usa el coco 343 actividades interactivas orientadas a su utilización en el Tercer Ciclo de la Educación Primaria. Pueden ser también útiles en el Primer Ciclo de la ESO.
Calculo21 ejercicios resueltos, paso a paso, de cálculo diferencial e integral, incluye foro y lista de correo de cálculo diferencial e integral.
http://www.ies.co.jp/math/java/index.html Colección de 279 Applets (Inglés)
http://www.fermatsi.org/ proporciona recursos matemáticos en español e inglés, para alumnos de Secundaria y Bachillerato. El portal muestra un amplio directorio de páginas que permiten al alumno y al profesor obtener información de interés sobre las matemáticas. Artículos de interés, asociaciones, educación especial e Historia de las matemáticas. Su autor es Fernando Sivit, profesor de enseñanza secundaria del IES "Francisco de Goya", de Madrid.
http://www.itcr.ac.cr/revistamate/ La Revista Matemática, Educación e Internet posee varias secciones, además de las contribuciones de los autores, tenemos las columnas: "El Mundo de las Matemáticas" para contar sobre matemáticas en general, "Aportes Pedagógicos y Material Didáctico" para el profesor que busca reflexiones y materiales en pedagogía, "Herramientas para Matemáticas e Internet" para los entusiastas que desean aprender a crear documentos para el Web, con animación e interacción, en el campo de las matemáticas, "Historia de las Matemáticas", "Juegos y Entretenimientos", "Problemas de Olimpiadas Matemáticas", "Foro Virtual en Enseñanza de la Matemáticas" , "Programación de Software Didáctico" y las nuevas secciones de "Multimedios" y "Calculadora en la Enseñanza".
Página de Loreto Ayuso dedicada a recoger recursos de interés en la red, para alumnos de matemáticas.
Matemáticas. Secundaria (ESO y Bachillerato) apuntes, ejercicios, applets Java...
Calcumat: ( Matemáticas con calculadoras gráficas y simbólicas) de Juan López Sánchez, gracias por el link...
IES Arroyo de la Miel de Benalmádena ( Málaga). Muy buena selección de actividades de matemática recreativa en el apartado "Taller de matemáticas". Excelentes colecciones de problemas en los apartados E.S.O. y Bachillerato.
Proyecto Tendris. Base de datos formada por exámenes propuestos por los profesores que componen el grupo de trabajo a sus alumnos de E.S.O. y de Bachillerato L.O.G.S.E. Combinatoria. Técnicas de recuento. Premiado por la Junta de Andalucía convocatoria 2004.
http://www.educaplus.org/modules/wfsection/viewarticles.php?category=4 Muchos temas interactivos, muy buena.
http://www.iescarrus.com/matematicas/edumat/ Portal dedicado a las matemáticas llevado adelante por el IES Carrús de Elche (España) a nivel educativo, donde podrás encontrar biografías de matemáticos, aplicaciones didácticas, apuntes, problemas online, profesor virtual, prensa, juegos online, enlaces, etc.
Departamento de Matemáticas e Informática IES La Rábida de Huelva ¡Completísima !
El Taller de las matemáticas del Colegio Jaime Balmes de Cieza (Murcia). http://www.colegio-jaimebalmes.com/mates/
WIRIS http://herramientas.educa.madrid.org/wiris/ es una herramienta de cálculo matemático accesible por Internet y con una amplia funcionalidad. Los usuarios acceden a una página web dónde plantean los cálculos deseados y reciben las respuestas instantes después. En la página oficial de WIRIS http://www.wiris.com/ encontrareis ejemplos y demos de lo que se puede hacer con esta aplicación ( en español. catalán e inglés)Manual de Wiris online en español .Pulsa aquí para descargar el tutorial básico en español.WIRIS en catalán: http://calculadora.edu365.com/
http://perso.wanadoo.es/paquipaginaweb/funciones/index.html Unidad didáctica de nivel de 4º de ESO: "Introducción a las funciones" que me envía Francisca Izquierdo Barragán, profesora de matemáticas en un centro TIC en El Viso del Alcor (Sevilla) . Incluye test de evaluación. es la primera web que hace, esta chica promete mucho enhorabuena. :-)
http://www.mismates.net web destinada a profesores, alumnos y todo aquel interesado en el mundo de las matemáticas. Contiene ejercicios, enciclopedias de términos matemáticos y astronómicos.
http://www.huascaran.edu.pe/recursos_ciencias/index.html unidades didácticas en formato Flash muy buenas de la página del Proyecto Huascarán programa estratégico del Ministerio de Educación de Perú , especializado en el uso educativo de las Tecnologías de la Información y Comunicación, (TIC)
http://www.aulademate.com/ Portal de Matemáticas para Bachillerato.
Departamento de matemáticas del IES Averroes de Córdoba
Curso de geometría para ESO, muy bueno http://mimosa.cnice.mecd.es/~clobo/index.htm
http://www.clarin.com/suplementos/informatica/2005/08/17/f-1034668.htm Amplia colección de enlaces a sitios dedicados a las matemáticas.
Departamento de Matemáticas del IES Mar Serena (Almería)
Matemáticas educativas http://www.iescarrus.com/edumat/
Portal dedicado a las matemáticas a nivel educativo, donde podrás encontrar biografías de matemáticos, aplicaciones didácticas, apuntes, problemas online, profesor virtual, prensa, juegos online, enlaces, etc.
http://www.sectormatematica.cl/ El Portal de las Matemáticas, de todo, completísima...
Recopilación de recursos realizada por Manuel Sada .
Ematematicas.net http://www.ematematicas.net/ Página destinada tanto a profesores como a alumnos de ESO y Bachillerato.. Los chicos podrán encontrar gran cantidad de ejercicios para hacer de forma interactiva.
Departamento de matemáticas del Colegio Virgen de Gracia de Granada. materiales para ESO y Bachillerato.
Aula matemática de Ábel Marín profesor de Matemáticas del IES Pérez de Ayala de Oviedo.
http://es.geocities.com/mundo_matematicas/ Matemáticas en tu mundo .
Conecto con las mates. Me puede venir muy bien para los alumnos que necesitan apoyo de 1º y 2º de ESO al igual que Los porcentajes.
El departamento de matemáticas del IES de Pravia (Asturias) publica en su web una serie de recursos para trabajar esta materia en ESO y Bachilerato. Además de programaciones y recursos para los distintos niveles, se recogen también orientaciones metodológicas y criterios de evaluación.
Refuerza y amplía tus matemáticas es un conjunto de páginas interactivas de Matemáticas, Aritmética, Álgebra y Problemas referidos a las citadas disciplinas, que se autogeneran y autocorrigen cada vez que se seleccionan, listas para ser utilizadas desde los navegadores más conocidos, Mozilla y Explorer, tanto en Guadalinex como en Windows, orientada principalmente al Refuerzo del Área de Matemáticas en el Primer Ciclo de la E.S.O. Lo que no excluye que sirva también como actividades para el Refuerzo y Ampliación tanto en Primaria como en Secundaria.
Materiales para construir la geometría (Primaria) Muy bueno.
http://www.amejor.com/mates/ Problemas matemáticos con "gancho" para primeros cursos de la ESO. Clasificados por ámbitos de contenido, con indicación de su grado de dificultas y las soluciones razonadas.
http://platea.pntic.mec.es/~aperez4/ Completísima página de Antonio Pérez Sanz del I.E.S. Salvador Dalí de Madrid. En ella encontrarás juegos, problemas, curiosidades, experiencias y materiales de aula, numerosos enlaces de interés...
Thales Página de la Sociedad andaluza de educación matemática. Se puede encontrar una amplia variedad de recursos didácticos.
Real Sociedad Matemática Web de la Real Sociedad Matemática Española. Publicaciones, convocatorias, debates, etc.
El Proyecto Descartes está desarrollado en el Centro Nacional de Información y Comunicación Educativa (CNICE) del Ministerio de Educación, Cultura y Deporte, para el uso de los profesores de Matemáticas en sus aulas. Se han desarrollado más de 100 Unidades Didácticas de Secundaria, y se pueden utilizar, no sólo en la web, sino que pueden descargarse los archivos a un ordenador local con suma facilidad.
Es una herramienta interactiva que permite al alumno mover puntos, cambiar parámetros, dibujar, y en definitiva actuar sobre una escena que puede presentar gráficas, puntos, figuras geométricas, textos, etc. directamente en una página web.
De mates ¿na? Elaborada por alumnos de 4º de ESO del instituto "SIERRA MINERA" de La Unión, Murcia.
Tablas Matemáticas de David Manura Página dedicada a las matemáticas, que incluye diversas secciones: Matemáticas generales, álgebra, geometría, trigonometría, cálculo, estadística, etc.... pueden ser descargas para verlas deconectado en un fichero .zip.
Las matemáticas de Mario teoría, problemas resueltos, biografías, lecturas recomendadas, etc.
http://www.linuxforkids.org/edu_math_sp.html Dirección con bastante software matemático para alumnos ACNEE que funcionan en Linux.
http://www.matematicas.net El paraíso de las matemáticas, imprescindible.
http://webs.uolsinectis.com.ar/acoda/apuntes.html Apuntes básicos de Matemáticas organizados por lecciones.
Portal chileno donde encontraras numerosos recursos y enlaces de interés.
OKmath, en este portal encontrarás cientos de problemas y ejercicios de matemáticas resueltos paso a paso.
http://nti.educa.rcanaria.es/matematicas/ página recopilada por Manuel de Armas Cruz. Colección de enlaces sobre diferentes aspectos de las matemáticas (historia, juegos, olimpiadas, software,...).
http://www.xtec.es/%7Ejcorder1/index.htm Matemáticas básicas de Primaria y ESO.
http://www.elosiodelosantos.com Este portal educativo cuenta con software educativo interactivo en línea y gratuito, con páginas para la resolución de problemas de matemáticas y con más de 12000 ejercicios resueltos.El acceso a los recursos es libre, gratuito y sin contraseñas
http://platea.pntic.mec.es/~jescuder/ Jesús ESCUDERO Profesor del I. E. S. Fray Luis de León de Salamanca) Acertijos, problemas, curiosidades...
2piMath de Jesus Plaza. Resúmenes, ejercicios, problemas, utilidades, software y enlaces.
Mis mates de Mª Dolores Rodríguez. Actividades para el aula, artículos, referencias de libros, etc.
Olimpiadas matemáticas . Todo sobre las Olimpiadas Matemáticas: qué son, convocatorias, información a los profesores, problemas de las últimas olimpiadas, material para la preparación,...
Gacetilla matemática. Contiene problemas, libros, anécdotas, información sobre los grandes matemáticos de la historia y enlaces con las mejores webs sobre la materia
http://platea.pntic.mec.es/~mzapata/matemat.htm de Miguel Zapata. Ejercicios, enlaces de interés...
http://roble.pntic.mec.es/~jbrihueg/ En esta página podrás encontrar actividades de clase y problemas para la Educación Secundaria(algunos de las Pruebas de acceso a la Universidad) organizados por temas y niveles.
Juegos y problemas de ingenio del club Mensa. Colección de los juegos de ingenio que se publican en las revistas y páginas web de Mensa.
http://www.ecomur.com Ecomur es un portal de economía y enseñanza dirigido a estudiantes y profesores de bachillerato, con recursos didácticos de las asignaturas de economía y enlaces educativos y económicos de interés. www.deberesmatematicas.com Herramientas didácticas específicas para la enseñanza y el aprendizaje de las matemáticas de la E.S.O. Ejercicios, problemas, exámenes, temarios, todos resueltos y explicados paso a paso. La suscripción para profesores es GRATUITA.Ejercicios de Matemáticas. Esta web ofrece una parte teórica y actividades resueltas que van a facilitar el aprendizaje. Cada uno de los apartados presenta unas herramientas para su desarrollo y ejercicios de repaso resueltos paso a paso, 3º- 4º E.S.O. http://www.ecobachillerato.com (Economía de Bachillerato) de Tomas Guajardo Cuervo. Multitud de materiales de interés para profesores y alumnos. Curiosidades Matemáticas.
Usa el coco 343 actividades interactivas orientadas a su utilización en el Tercer Ciclo de la Educación Primaria. Pueden ser también útiles en el Primer Ciclo de la ESO.
Calculo21 ejercicios resueltos, paso a paso, de cálculo diferencial e integral, incluye foro y lista de correo de cálculo diferencial e integral.
http://www.ies.co.jp/math/java/index.html Colección de 279 Applets (Inglés)
http://www.fermatsi.org/ proporciona recursos matemáticos en español e inglés, para alumnos de Secundaria y Bachillerato. El portal muestra un amplio directorio de páginas que permiten al alumno y al profesor obtener información de interés sobre las matemáticas. Artículos de interés, asociaciones, educación especial e Historia de las matemáticas. Su autor es Fernando Sivit, profesor de enseñanza secundaria del IES "Francisco de Goya", de Madrid.
http://www.itcr.ac.cr/revistamate/ La Revista Matemática, Educación e Internet posee varias secciones, además de las contribuciones de los autores, tenemos las columnas: "El Mundo de las Matemáticas" para contar sobre matemáticas en general, "Aportes Pedagógicos y Material Didáctico" para el profesor que busca reflexiones y materiales en pedagogía, "Herramientas para Matemáticas e Internet" para los entusiastas que desean aprender a crear documentos para el Web, con animación e interacción, en el campo de las matemáticas, "Historia de las Matemáticas", "Juegos y Entretenimientos", "Problemas de Olimpiadas Matemáticas", "Foro Virtual en Enseñanza de la Matemáticas" , "Programación de Software Didáctico" y las nuevas secciones de "Multimedios" y "Calculadora en la Enseñanza".
Página de Loreto Ayuso dedicada a recoger recursos de interés en la red, para alumnos de matemáticas.
Matemáticas. Secundaria (ESO y Bachillerato) apuntes, ejercicios, applets Java...
Calcumat: ( Matemáticas con calculadoras gráficas y simbólicas) de Juan López Sánchez, gracias por el link...
IES Arroyo de la Miel de Benalmádena ( Málaga). Muy buena selección de actividades de matemática recreativa en el apartado "Taller de matemáticas". Excelentes colecciones de problemas en los apartados E.S.O. y Bachillerato.
Proyecto Tendris. Base de datos formada por exámenes propuestos por los profesores que componen el grupo de trabajo a sus alumnos de E.S.O. y de Bachillerato L.O.G.S.E. Combinatoria. Técnicas de recuento. Premiado por la Junta de Andalucía convocatoria 2004.
http://www.educaplus.org/modules/wfsection/viewarticles.php?category=4 Muchos temas interactivos, muy buena.
http://www.iescarrus.com/matematicas/edumat/ Portal dedicado a las matemáticas llevado adelante por el IES Carrús de Elche (España) a nivel educativo, donde podrás encontrar biografías de matemáticos, aplicaciones didácticas, apuntes, problemas online, profesor virtual, prensa, juegos online, enlaces, etc.
Departamento de Matemáticas e Informática IES La Rábida de Huelva ¡Completísima !
El Taller de las matemáticas del Colegio Jaime Balmes de Cieza (Murcia). http://www.colegio-jaimebalmes.com/mates/
WIRIS http://herramientas.educa.madrid.org/wiris/ es una herramienta de cálculo matemático accesible por Internet y con una amplia funcionalidad. Los usuarios acceden a una página web dónde plantean los cálculos deseados y reciben las respuestas instantes después. En la página oficial de WIRIS http://www.wiris.com/ encontrareis ejemplos y demos de lo que se puede hacer con esta aplicación ( en español. catalán e inglés)Manual de Wiris online en español .Pulsa aquí para descargar el tutorial básico en español.WIRIS en catalán: http://calculadora.edu365.com/
http://perso.wanadoo.es/paquipaginaweb/funciones/index.html Unidad didáctica de nivel de 4º de ESO: "Introducción a las funciones" que me envía Francisca Izquierdo Barragán, profesora de matemáticas en un centro TIC en El Viso del Alcor (Sevilla) . Incluye test de evaluación. es la primera web que hace, esta chica promete mucho enhorabuena. :-)
http://www.mismates.net web destinada a profesores, alumnos y todo aquel interesado en el mundo de las matemáticas. Contiene ejercicios, enciclopedias de términos matemáticos y astronómicos.
http://www.huascaran.edu.pe/recursos_ciencias/index.html unidades didácticas en formato Flash muy buenas de la página del Proyecto Huascarán programa estratégico del Ministerio de Educación de Perú , especializado en el uso educativo de las Tecnologías de la Información y Comunicación, (TIC)
http://www.aulademate.com/ Portal de Matemáticas para Bachillerato.
Departamento de matemáticas del IES Averroes de Córdoba
Curso de geometría para ESO, muy bueno http://mimosa.cnice.mecd.es/~clobo/index.htm
http://www.clarin.com/suplementos/informatica/2005/08/17/f-1034668.htm Amplia colección de enlaces a sitios dedicados a las matemáticas.
Departamento de Matemáticas del IES Mar Serena (Almería)
Matemáticas educativas http://www.iescarrus.com/edumat/
Portal dedicado a las matemáticas a nivel educativo, donde podrás encontrar biografías de matemáticos, aplicaciones didácticas, apuntes, problemas online, profesor virtual, prensa, juegos online, enlaces, etc.
http://www.sectormatematica.cl/ El Portal de las Matemáticas, de todo, completísima...
Recopilación de recursos realizada por Manuel Sada .
Ematematicas.net http://www.ematematicas.net/ Página destinada tanto a profesores como a alumnos de ESO y Bachillerato.. Los chicos podrán encontrar gran cantidad de ejercicios para hacer de forma interactiva.
Departamento de matemáticas del Colegio Virgen de Gracia de Granada. materiales para ESO y Bachillerato.
Aula matemática de Ábel Marín profesor de Matemáticas del IES Pérez de Ayala de Oviedo.
http://es.geocities.com/mundo_matematicas/ Matemáticas en tu mundo .
Conecto con las mates. Me puede venir muy bien para los alumnos que necesitan apoyo de 1º y 2º de ESO al igual que Los porcentajes.
El departamento de matemáticas del IES de Pravia (Asturias) publica en su web una serie de recursos para trabajar esta materia en ESO y Bachilerato. Además de programaciones y recursos para los distintos niveles, se recogen también orientaciones metodológicas y criterios de evaluación.
EINMAHL UTILIZA LA TEORÍA DE LOS VALORES EXTREMOS
Un matemático calcula el récord definitivo de los 100 metros en 9.29
El matemático holandés John Einmahl, de la Universidad de Tilburgo, ha calculado el 'récord definitivo' de 14 disciplinas atléticas y, entre ellas, el masculino de los 100 metros que él estima en 9.29 segundos apoyándose en la teoría de los valores extremos y en proyecciones estadísticas.
Einmahl no pretende predecir los récords posibles en un futuro lejano sino, como lo dice expresamente su estudio, los récords que podrían darse bajo las condiciones actuales. La base de los cálculos de Einmahl son las mejores marcas de 1.546 atletas masculinos y 1024 atletas femeninas de elite de cada disciplina estudiada que luego somete a complicadas elaboraciones matemáticas con ayuda de un ordenador.
Los resultados no sólo le permiten determinar el récord "definitivo" de cada disciplina sino además ver el valor de un récord actual en comparación con lo que sería teóricamente posible, y también comparar las mejores marcas de diferentes disciplinas, atendiendo a lo que las separa de su nivel ideal.
Según los cálculos de Einmahl, el récord del maratón entre los hombres, que posee el keniano Paul Tergat (2h.04:55) es especialmente notable puesto que el matemático holandés considera que sólo podría ser mejorado en 49 segundos. Entre las mujeres, en cambio, el récord de la británica Paula Radcliffe, de 2h.15:25, podría ser claramente mejorado en 8 minutos y 50 segundos.
Curiosamente, también en las pruebas de velocidad, en las que habitualmente se cree que se está muy cerca del límite de lo humanamente posible, los cálculos de Einmahl apuntan a posibles mejoras. No sólo el récord de los 100 metros, que podría ser bajado de los 9.77 de Asafa Powell a 9.29, podría mejorar sino también el récord de 200 metros, en manos de Michael Johnson en 19.32, está casi un segundo por encima de lo posible.
En el lanzamiento de jabalina las mujeres parecen estar más cerca del ideal que los hombres. Mientras que el récord de la cubana Osleydis Menéndez, de 71 metros y 70 centímetros, podría mejorarse apenas en 80 centímetros, el del checo Jan Zelezny, de 98,48, podría mejorarse en 8 metros y 2 centímetros.
La teoría de los valores extremos, la especialidad de Einmahl, suele utilizarse para calcular cosas como "la mayor pérdida posible" en caso de catástrofes naturales, por lo que las compañías de seguros recurren con frecuencia a esta disciplina para determinar el monto de sus pólizas. Einmahl también ha empleado esa disciplina para predecir el comportamiento de las acciones en los mercados bursátiles.
Un matemático calcula el récord definitivo de los 100 metros en 9.29
El matemático holandés John Einmahl, de la Universidad de Tilburgo, ha calculado el 'récord definitivo' de 14 disciplinas atléticas y, entre ellas, el masculino de los 100 metros que él estima en 9.29 segundos apoyándose en la teoría de los valores extremos y en proyecciones estadísticas.
Einmahl no pretende predecir los récords posibles en un futuro lejano sino, como lo dice expresamente su estudio, los récords que podrían darse bajo las condiciones actuales. La base de los cálculos de Einmahl son las mejores marcas de 1.546 atletas masculinos y 1024 atletas femeninas de elite de cada disciplina estudiada que luego somete a complicadas elaboraciones matemáticas con ayuda de un ordenador.
Los resultados no sólo le permiten determinar el récord "definitivo" de cada disciplina sino además ver el valor de un récord actual en comparación con lo que sería teóricamente posible, y también comparar las mejores marcas de diferentes disciplinas, atendiendo a lo que las separa de su nivel ideal.
Según los cálculos de Einmahl, el récord del maratón entre los hombres, que posee el keniano Paul Tergat (2h.04:55) es especialmente notable puesto que el matemático holandés considera que sólo podría ser mejorado en 49 segundos. Entre las mujeres, en cambio, el récord de la británica Paula Radcliffe, de 2h.15:25, podría ser claramente mejorado en 8 minutos y 50 segundos.
Curiosamente, también en las pruebas de velocidad, en las que habitualmente se cree que se está muy cerca del límite de lo humanamente posible, los cálculos de Einmahl apuntan a posibles mejoras. No sólo el récord de los 100 metros, que podría ser bajado de los 9.77 de Asafa Powell a 9.29, podría mejorar sino también el récord de 200 metros, en manos de Michael Johnson en 19.32, está casi un segundo por encima de lo posible.
En el lanzamiento de jabalina las mujeres parecen estar más cerca del ideal que los hombres. Mientras que el récord de la cubana Osleydis Menéndez, de 71 metros y 70 centímetros, podría mejorarse apenas en 80 centímetros, el del checo Jan Zelezny, de 98,48, podría mejorarse en 8 metros y 2 centímetros.
La teoría de los valores extremos, la especialidad de Einmahl, suele utilizarse para calcular cosas como "la mayor pérdida posible" en caso de catástrofes naturales, por lo que las compañías de seguros recurren con frecuencia a esta disciplina para determinar el monto de sus pólizas. Einmahl también ha empleado esa disciplina para predecir el comportamiento de las acciones en los mercados bursátiles.
lunes, diciembre 18, 2006
TRES AMIGOS
Tres amigos se ubican en fila. El primero dice 3, el segundo dice 6, el tercero dice 9, el primero dice 12 y siguen contando de tres en tres.Juan dice 27, Esteban el 75 y Ana el 42.
¿Quién dice el 291 si siguen contando en el mismo orden? Explica por qué
¿Quién dice el 291 si siguen contando en el mismo orden? Explica por qué
ALBERTO COTO Record Guinness
http://www.albertocoto.com/
El asturiano Alberto Coto es la persona más rápida del Mundo haciendo cálculos mentales, como así lo certifica el Libro Guinness de los Records.Su habilidad innata le permite desarrollar todo tipo de cálculos a velocidades de vértigo, superando incluso la velocidad de la máquina, lo que hace de sus exhibiciones algo único e inolvidable para quien lo presencia
El asturiano Alberto Coto es la persona más rápida del Mundo haciendo cálculos mentales, como así lo certifica el Libro Guinness de los Records.Su habilidad innata le permite desarrollar todo tipo de cálculos a velocidades de vértigo, superando incluso la velocidad de la máquina, lo que hace de sus exhibiciones algo único e inolvidable para quien lo presencia
domingo, diciembre 17, 2006
ARITMÉTICA
18. Pablo eligió tres dígitos distintos y escribió todos los números de tres cifras que se forman con ellos (sin repeticiones). Luego sumó todos los números que obtuvo. Hallar la suma de Pablo, sabiendo que la suma de los dígitos originales es 14.
19. Hallar el menor número entero positivo tal que 5 veces el producto de sus cifras sea igual al número.
20. Sea A un conjunto de números naturales tal que:
1) Todos sus elementos son menores que 1000.
2) Ninguno de sus elementos es un cuadrado perfecto
3) El producto de dos cualesquiera de sus elementos es un cuadrado perfecto
¿Cuál es el mayor número de elementos que S puede tener?
21. En una urna se colocan 900 tarjetas del 100 al 999 y se mezclan perfectamente. Le pedimos a Julia que saque una tarjeta, anote la suma de los dígitos del número que sacó y rompa la tarjeta. ¿Cuál es el menor número de veces que debemos pedirle a Julia que repita esa operación para estar seguros de que anotará al menos tres veces la misma suma?
22. El boleto de entrada a un concierto a beneficio del Instituto Rioplatense de Promoción de la Matemática era un donativo de una cantidad entera menor que 500 pesos. Asistieron al concierto 1997 personas, entre argentinos, chilenos, uruguayos y brasileños.
a) Demuestra que hubo al menos dos personas de la misma nacionalidad que pagaron lo mismo.
b) Si el mayor número de veces que se repitió un donativo fue 10, se compraron boletos de cada uno de los precios y la cantidad recaudada fue la menor posible ¿cuántos boletos de cada uno de los precios se compraron?
Un número capicúa es aquel que se lee igual de izquierda a derecha que de derecha a izquierda, por ejemplo el número 4093904 es capicúa.
19. Hallar el menor número entero positivo tal que 5 veces el producto de sus cifras sea igual al número.
20. Sea A un conjunto de números naturales tal que:
1) Todos sus elementos son menores que 1000.
2) Ninguno de sus elementos es un cuadrado perfecto
3) El producto de dos cualesquiera de sus elementos es un cuadrado perfecto
¿Cuál es el mayor número de elementos que S puede tener?
21. En una urna se colocan 900 tarjetas del 100 al 999 y se mezclan perfectamente. Le pedimos a Julia que saque una tarjeta, anote la suma de los dígitos del número que sacó y rompa la tarjeta. ¿Cuál es el menor número de veces que debemos pedirle a Julia que repita esa operación para estar seguros de que anotará al menos tres veces la misma suma?
22. El boleto de entrada a un concierto a beneficio del Instituto Rioplatense de Promoción de la Matemática era un donativo de una cantidad entera menor que 500 pesos. Asistieron al concierto 1997 personas, entre argentinos, chilenos, uruguayos y brasileños.
a) Demuestra que hubo al menos dos personas de la misma nacionalidad que pagaron lo mismo.
b) Si el mayor número de veces que se repitió un donativo fue 10, se compraron boletos de cada uno de los precios y la cantidad recaudada fue la menor posible ¿cuántos boletos de cada uno de los precios se compraron?
Un número capicúa es aquel que se lee igual de izquierda a derecha que de derecha a izquierda, por ejemplo el número 4093904 es capicúa.
ARITMÉTICA
8. ¿Cuál es el menor número natural por el que debemos multiplicar 504 para obtener un cuadrado perfecto?
9. Se sabe que el producto de tres números enteros positivos es 180. Si se sabe que dos de los números son iguales, ¿cuál es el menor valor que puede tomar la suma de los tres números?
10. ¿De cuántas maneras se puede escribir el número 7800 como producto de dos factores enteros positivos?
11. Probar que el número abcabc es múltiplo de 7, de 11 y de 13.
12. Probar que ninguno de los enteros 1573, 15731573, 157315731573, etc., es un número primo.
13. Determine todos los pares de números que tienen el mismo máximo común divisor y mínimo común múltiplo que el par de números 1470 y 126.
14. Hallar un número de 3 cifras ab6 sabiendo que las tres últimas cifras de ( ab6)2 son ab6.
15. Un número de 5 cifras que termina en 7 se pasó 4 números de un capicúa y le faltan 7 números para el siguiente capicúa (Un número capicúa es aquel que se lee igual de izquierda a derecha y viceversa, por ejemplo: 4093904). ¿Qué número es?
9. Se sabe que el producto de tres números enteros positivos es 180. Si se sabe que dos de los números son iguales, ¿cuál es el menor valor que puede tomar la suma de los tres números?
10. ¿De cuántas maneras se puede escribir el número 7800 como producto de dos factores enteros positivos?
11. Probar que el número abcabc es múltiplo de 7, de 11 y de 13.
12. Probar que ninguno de los enteros 1573, 15731573, 157315731573, etc., es un número primo.
13. Determine todos los pares de números que tienen el mismo máximo común divisor y mínimo común múltiplo que el par de números 1470 y 126.
14. Hallar un número de 3 cifras ab6 sabiendo que las tres últimas cifras de ( ab6)2 son ab6.
15. Un número de 5 cifras que termina en 7 se pasó 4 números de un capicúa y le faltan 7 números para el siguiente capicúa (Un número capicúa es aquel que se lee igual de izquierda a derecha y viceversa, por ejemplo: 4093904). ¿Qué número es?
Aritmética
1. La suma de tres números enteros positivos desconocidos es 12. Hallar el número más pequeño que se puede obtener multiplicando estos tres números
2. Suponemos que todo número de siete dígitos es un posible número telefónico, excepto si comienza con 0 ó ¿Cuál es la fracción de números telefónicos que comienzan con 9 y terminan con 0?
3. A y B son dos números enteros diferentes escogidos entre 1 y 40 inclusive. ¿Cuál es el mayor valor que puede tomar la siguiente expresión? (a*b)/(a-b)
4. La suma de seis números es par, el producto de los cuatro primeros es impar y el último es par. ¿El quinto número es par o impar?
5. Carlos tiene un cierto número de monedas de colección. Cuando ordena las monedas en montones de 5, no le sobra ninguna moneda. Cuando las ordena en montones de a 6, tampoco le sobran monedas. Pero si las ordena en montones de 7, le sobra una moneda. ¿Cuál es el menor número de monedas que puede tener Carlos?
6. ¿Cuáles son las últimas dos cifras de 2 222 ?
2. Suponemos que todo número de siete dígitos es un posible número telefónico, excepto si comienza con 0 ó ¿Cuál es la fracción de números telefónicos que comienzan con 9 y terminan con 0?
3. A y B son dos números enteros diferentes escogidos entre 1 y 40 inclusive. ¿Cuál es el mayor valor que puede tomar la siguiente expresión? (a*b)/(a-b)
4. La suma de seis números es par, el producto de los cuatro primeros es impar y el último es par. ¿El quinto número es par o impar?
5. Carlos tiene un cierto número de monedas de colección. Cuando ordena las monedas en montones de 5, no le sobra ninguna moneda. Cuando las ordena en montones de a 6, tampoco le sobran monedas. Pero si las ordena en montones de 7, le sobra una moneda. ¿Cuál es el menor número de monedas que puede tener Carlos?
6. ¿Cuáles son las últimas dos cifras de 2 222 ?
PROBLEMA
Encuentra todos los valores de X tales que
1! + 2! + 3! + 4! + ..... +x! sea un cuadrado perfecto.
1! + 2! + 3! + 4! + ..... +x! sea un cuadrado perfecto.
viernes, diciembre 15, 2006
DEL 1 AL 9
¿ Cómo escribirías los dígitos del 1 al 9 y en ese mismo orden, intercalando los signos aritméticos que quieras para que el resultado sea 100?
CON CUATRO CUATROS
Utilizando únicamente cuatro cuatros y todas las operaciones que conozcas, además de paréntesis, intenta escribir todos los números del 0 al 10, ambos incluidos.
El número 24 se puede escribir utilizando únicamente tres ochos así: 24= 8+8+8.
¿Podrías escribirlo utilizando únicamente tres treses? ¿Y utilizando tres doses?
miércoles, diciembre 13, 2006
Las Iguanas
Las Iguanas
Inteligentes Iguanas
Imaginan Insólitas e Increíbles Ideas
Usa las 5 claves para resolver este problema:
Los niños encontraron un nido con 5 huevos de Iguana numerados del 1 al 6.
Los huevos se fueron abriendo uno después del otro.
Los huevos con números pares se abrieron 2 minutos después del anterior.
Los huevos con números impares se abrieron 5 minutos después del huevo anterior.
El huevo número 5 se abrió de primero.
¿Cuánto duraron los huevos en abrirse?
¿Qué pasaría si se abre el huevo número 2 de primero?
Inteligentes Iguanas
Imaginan Insólitas e Increíbles Ideas
Usa las 5 claves para resolver este problema:
Los niños encontraron un nido con 5 huevos de Iguana numerados del 1 al 6.
Los huevos se fueron abriendo uno después del otro.
Los huevos con números pares se abrieron 2 minutos después del anterior.
Los huevos con números impares se abrieron 5 minutos después del huevo anterior.
El huevo número 5 se abrió de primero.
¿Cuánto duraron los huevos en abrirse?
¿Qué pasaría si se abre el huevo número 2 de primero?
Los Tiburones
Los Tiburones
Temibles Tiburones
Tomando Tazas de Té
Tras la Tempestad
Usa las 4 claves para resolver este problema:
En una reunión de tiburones sólo había 13 tazas de té.
Todos los tiburones que tomaron té antes de la tempestad, tomaron 3 tazas de té cada uno.
Todos los tiburones que tomaron té tras la tempestad tomaron 2 tazas de té cada uno.
Solo un tiburón tomó té antes y después de la tormenta.
¿Cuántos tiburones tomaron té?
Esta pregunta tiene al menos 2 respuestas correctas.
Temibles Tiburones
Tomando Tazas de Té
Tras la Tempestad
Usa las 4 claves para resolver este problema:
En una reunión de tiburones sólo había 13 tazas de té.
Todos los tiburones que tomaron té antes de la tempestad, tomaron 3 tazas de té cada uno.
Todos los tiburones que tomaron té tras la tempestad tomaron 2 tazas de té cada uno.
Solo un tiburón tomó té antes y después de la tormenta.
¿Cuántos tiburones tomaron té?
Esta pregunta tiene al menos 2 respuestas correctas.
Los Perezosos
Los Perezosos
Perezosos Perchados
Pidiendo Permiso Para Pasar
Usa las 5 claves para resolver este problema:
La suma de los ojos de los perezosos es un número par, pero el número de perezosos es impar.
El número de perezosos no es un número primo.
El número de perezosos es menor a 10.
El número de perezosos es un múltiplo de 3.
El resultado de la suma de las patas de los perezosos es mayor que 30.
¿Cuántos perezosos tenemos?
Perezosos Perchados
Pidiendo Permiso Para Pasar
Usa las 5 claves para resolver este problema:
La suma de los ojos de los perezosos es un número par, pero el número de perezosos es impar.
El número de perezosos no es un número primo.
El número de perezosos es menor a 10.
El número de perezosos es un múltiplo de 3.
El resultado de la suma de las patas de los perezosos es mayor que 30.
¿Cuántos perezosos tenemos?
Las Mariposas
Las Mariposas
Maravillosas Mariposas Manchadas Mordiendo Moras Maduras
Usa las 5 claves para resolver este problema:
Hay más arañas que insectos en el dibujo.
El número de arañas y el de insectos son ambos impares.
Si sumamos las arañas y los insectos tendremos un total de 12 invertebrados.
Las arañas tienen 2 patas más que los insectos.
Si sumamos todas las patas de las arañas y le restamos 26, tendremos el número de patas de los insectos.
¿Cuántos insectos tenemos?
Maravillosas Mariposas Manchadas Mordiendo Moras Maduras
Usa las 5 claves para resolver este problema:
Hay más arañas que insectos en el dibujo.
El número de arañas y el de insectos son ambos impares.
Si sumamos las arañas y los insectos tendremos un total de 12 invertebrados.
Las arañas tienen 2 patas más que los insectos.
Si sumamos todas las patas de las arañas y le restamos 26, tendremos el número de patas de los insectos.
¿Cuántos insectos tenemos?
La Lora
La Lora
Lora Leyendo Largos Libros Líricos Lentamente
Usa las 4 claves para resolver este problema:
La lora se llevó 11 libros para leer en sus vacaciones.
La lora lee 1/4 de libro por noche de lunes a viernes.
Los sábados y domingos tiene más tiempo y lee 3/8 de libro cada día.
La tercer semana la lora se enfermó (de lunes a domingo) y sólo pudo leer la mitad de lo acostumbrado.
¿Cuántos días tardará en leer todos los libros?
Lora Leyendo Largos Libros Líricos Lentamente
Usa las 4 claves para resolver este problema:
La lora se llevó 11 libros para leer en sus vacaciones.
La lora lee 1/4 de libro por noche de lunes a viernes.
Los sábados y domingos tiene más tiempo y lee 3/8 de libro cada día.
La tercer semana la lora se enfermó (de lunes a domingo) y sólo pudo leer la mitad de lo acostumbrado.
¿Cuántos días tardará en leer todos los libros?
Los Cocodrilitos
Los Cocodrilitos
Cocodrilos Cantando Canciones de Cuna Consolando Crias
Usa las 4 claves para resolver este problema:
El número de cocodrilitos es un número impar.
El cantante está acurrucando a uno. La suma del resto de cocodrilitos es un múltiplo de 4.
El número de cocodrilitos es mayor a 3 y menor a 13.
El número total de cocodrilitos es un multiplo de 3.
¿Cuántos cocodrilitos tenemos?
Cocodrilos Cantando Canciones de Cuna Consolando Crias
Usa las 4 claves para resolver este problema:
El número de cocodrilitos es un número impar.
El cantante está acurrucando a uno. La suma del resto de cocodrilitos es un múltiplo de 4.
El número de cocodrilitos es mayor a 3 y menor a 13.
El número total de cocodrilitos es un multiplo de 3.
¿Cuántos cocodrilitos tenemos?
miércoles, octubre 18, 2006
JUEGO
Os propongo un pasatiempo, tenéis que dividir en cuatro partes iguales sin que os sobre ningún trozo la siguiente figura geométrica.
COLOCAR NÚMEROS
Colocar los numerillos del uno al seis, de forma que la suma de cada lado del triángulo sea igual.
NÚMEROS ROMANOS
Hoy quiero plagiar de la página Huevo de chocolate, ideal para peques, tres acertijos de los que cuelga en la sección de números romanos los cuales son originales:
01. Cinco más uno y quinientos te dará, querido amigo, una planta y no te miento.
02. ¿Qué país se queda en 1090 si le quitan las vocales?
03. Si digo: "uno entre veinte es igual a diecinueve", ¿es posible?
01. Cinco más uno y quinientos te dará, querido amigo, una planta y no te miento.
02. ¿Qué país se queda en 1090 si le quitan las vocales?
03. Si digo: "uno entre veinte es igual a diecinueve", ¿es posible?
jueves, septiembre 14, 2006
jueves, septiembre 07, 2006
ECUACIONES...
Cómo resolver una ecuación de primer grado
Ecuaciones de primer grado
Dada la ecuación ax + b = 0, hay que realizar dos pasos:
1º. Pasar el término independiente, b, al segundo miembro cambiándolo de signo.
ax = -b
2º. Pasar, dividiendo, el coeficiente de x, a, al segundo miembro.
x = -b/a
Ejemplo
1Resolver 2x + 6 = 0
Primer paso: 2x = -6
Segundo paso: x = -6/2 = -3
SOLUCIÓN: x = -3
COMPROBACIÓN:
2·(-3) + 6 = -6 + 6 = 0
Ejemplo 2
Resolver 2x - 6 = 0
Primer paso: 2x = -(-6) = 6
Segundo paso: x = 6/2 = 3
SOLUCIÓN: x = 3
COMPROBACIÓN:
2 · 3 - 6 = 6 - 6 = 0
Ecuaciones de primer grado
Dada la ecuación ax + b = 0, hay que realizar dos pasos:
1º. Pasar el término independiente, b, al segundo miembro cambiándolo de signo.
ax = -b
2º. Pasar, dividiendo, el coeficiente de x, a, al segundo miembro.
x = -b/a
Ejemplo
1Resolver 2x + 6 = 0
Primer paso: 2x = -6
Segundo paso: x = -6/2 = -3
SOLUCIÓN: x = -3
COMPROBACIÓN:
2·(-3) + 6 = -6 + 6 = 0
Ejemplo 2
Resolver 2x - 6 = 0
Primer paso: 2x = -(-6) = 6
Segundo paso: x = 6/2 = 3
SOLUCIÓN: x = 3
COMPROBACIÓN:
2 · 3 - 6 = 6 - 6 = 0
domingo, agosto 20, 2006
NOTICIA:El 'Bobby Fischer' de las matemáticas
El ruso Perelman, que resolvió la conjetura de Poincaré, un problema del milenio, será el gran ausente de la reunión de Madrid
A partir del próximo martes, unos 4.000 matemáticos de todo el mundo acudirán, según una tradición iniciada hace más de 100 años, a su cita cuatrienal, que, por primera vez, será en Madrid. La estrella de este Congreso Internacional de Matemáticos es la conjetura de Henri Poincaré, enunciada en 1904 por el célebre matemático francés, que es muy posible que se dé finalmente por demostrada. La conjetura de Poincaré se refiere a las esferas de cuatro dimensiones, unos objetos no sólo inexistentes, sino también inimaginables para el común de los mortales. El principal responsable y probable ganador el martes de una medalla Fields (equivalente al Nobel) es el matemático ruso Grigori Perelman, que será el gran ausente de la cita de Madrid a pesar de haber sido él quien propuso una solución a dicha conjetura tras pasar encerrado 24 horas sobre 24 en su habitación de San Petersburgo para resolverla. O tal vez precisamente por ello.
Los organizadores del congreso no tienen casi esperanzas de que Perelman se presente en Madrid, pero eso no ha evitado que arrecien los rumores sobre su elección para una de las medallas Fields que se anunciarán el martes junto a los premios Nevanlinna y Gauss, otorgado por primera vez este año. Todos estos galardones serán entregados por el rey Juan Carlos.
Perelman, hijo de matemático, ha dejado el mundanal ruido desde que en 2003 recorrió instituciones de Estados Unidos explicando su método, que presentó en Internet sin previo aviso en 2002. Se cree que sigue viviendo en San Petersburgo, pero ya no trabaja en el Instituto Steklov. Sus compañeros allí han asegurado al diario Izvestia que no le importan los premios ni el dinero, informa Efe: "Es un hombre ensimismado, a veces da la impresión de estar un poco chiflado; no es un defecto, sino una cualidad propia de todos los buenos matemáticos", ha dicho Yevgueni Damaskinski. "Creo que está pensando ya en otra cosa, pero es un genio; su trabajo es espectacular. Yo le comparo con el ajedrecista Bobby Fischer", comenta Manuel de León, presidente del comité organizador del Congreso de Matemáticos.
En los últimos tres meses se han presentado tres estudios de matemáticos prestigiosos que completan el trabajo de Perelman (que no sólo demostraría la conjetura de Poincaré, sino la más amplia conjetura de geometrización de Thurston), miles de páginas para algo que puede plantearse brevemente pero que se ha resistido más de 100 años y significaría un verdadero avance científico. Los matemáticos coinciden en que la solución permitiría, por ejemplo, llegar a conocer la forma del Universo.
Se trata de un problema de topología (que estudia las formas geométricas) sobre la cantidad de superficies de tres dimensiones que existen. Poincaré dijo que "el resultado obtenido para la esfera n=2 del espacio de dimensión 3 tenía un análogo para la esfera n=3 del espacio de dimensión 4". Con ello sugirió que cualquier forma compacta que no tuviera agujeros sería equivalente a una esfera. En una superficie así, un lazo podría encogerse (como una goma elástica) hasta convertirse en un punto, deformando la superficie pero sin romperla ni agujerearla. En dos dimensiones se ve clara la diferencia entre las superficies de una esfera y un toro (como un donut, con agujero en medio), pero en las de tres dimensiones no se pueden ver los agujeros, imposible dibujarlas.
"¿Cómo se decide si algo es correcto?", se pregunta John Ball, presidente de la Unión Matemática Internacional, en la revista Nature, refiriéndose a Perelman. "Sólo que gente inteligente, expertos, lo lean y lleguen a una opinión". Y su opinión es positiva. "Estoy convencido de que Perelman ha demostrado la conjetura", dice John Morgan, uno de los que han intentado encontrar fallos en el trabajo del ruso y que explicará el suyo en Madrid junto a Richard Hamilton, sobre cuya labor se ha basado Perelman. Por primera vez, será también conferenciante plenario un matemático español, Juan Luis Vázquez. Una de las razones para que corran los rumores sobre una medalla Fields para Perelman es que nació en 1966 y estos galardones son para matemáticos de hasta 40 años. También optaría a ganar un millón de dólares por haber resuelto el primero de los siete problemas del milenio planteados por el Instituto Clay, cuyos representantes estarán en Madrid.
sábado, agosto 19, 2006
UNA BONITA HISTORIA SOBRE GAUSS
"...Gauss cuando a la edad de 10 años un profesor le ordenó a él y a toda su clase que sumaran todos los números enteros desde el 1 al 100. El maestro pensó que la tarea mantendría acupada por un buen rato a la clase, pero a los poco minutos Gauss se levantó con el número 5.050 escrito en su pizarra sin ningún otro desarrollo aritmético. ¿El truco?, bueno imaginó que escribía dos veces, al derecho y al revés, una secuencia encima de otra:
1 + 2 + 3 + 4 + ......... + 97 + 98 + 99 + 100
100 + 99 + 98 + 97 + ........ + 4 + 3 + 2 + 1
Al sumar obtenía cien pares igual a 101 y al sumar estos para luego dividir en 2 llegaba a la suma requerida...."
1 + 2 + 3 + 4 + ......... + 97 + 98 + 99 + 100
100 + 99 + 98 + 97 + ........ + 4 + 3 + 2 + 1
Al sumar obtenía cien pares igual a 101 y al sumar estos para luego dividir en 2 llegaba a la suma requerida...."
miércoles, agosto 16, 2006
DOS RETOS PARA MAYORES....
1- ¿Es posible utilizar seis (6) dígitos diferentes para formar dos números "primos" que sumados den un total de 1.000?
2- ¿Es posible utilizar ocho (8) dígitos diferentes para formar dos números "primos" que sumados den un total de 10.000?
2- ¿Es posible utilizar ocho (8) dígitos diferentes para formar dos números "primos" que sumados den un total de 10.000?
lunes, julio 31, 2006
UNA CURIOSIDAD
Elegir tres cifras entre el 0 y el 9, que no esten repetidas, por ejemplo, 2 3 8.
Le damos la vuelta y restamos al mayor el menor: 8 3 2 - 2 3 8 = 5 9 4.
Le damos la vuelta y esta vez los sumamos: 4 9 5 + 5 9 4 = 1 0 8 9.
Siempre da 1089. Con cualesquiera tres cifras
Le damos la vuelta y restamos al mayor el menor: 8 3 2 - 2 3 8 = 5 9 4.
Le damos la vuelta y esta vez los sumamos: 4 9 5 + 5 9 4 = 1 0 8 9.
Siempre da 1089. Con cualesquiera tres cifras
viernes, julio 14, 2006
JUEGO DEL 100
Eder y Elena juegan al juego del 100. Se empieza diciendo el número 3. En cada jugada se debe decir un número mayor que el último que se haya dicho pero menor que su doble. Gana quien diga el 100. Encuentra una estrategia ganadora.
FOCOS
Tenemos 10 focos. Al tocar uno de ellos todos cambian, el foco encendido se apaga y el foco apagado se enciende, excepto el foco que se toca, que permanece como estaba. Se empieza con todos los focos encendidos. Explica que tienes que hacer para lograr que se apaguen todos los focos.
EDADES DE LOS HIJOS
Un hombre tiene tres hijos.El producto de las edades de sus hijos es 1664. El menor de ellos tiene al menos la mitad de la edad del mayor.¿Cuál es la sUma de las edades de sus hijos?
TRIANGULOS
¿ Cuántos Triángulos diferentes contiene la siguiente figura? Por ejemplo AFB,AGB,ACB,BFG,BFC y BGC son seis triángulos distintos.Es conveniente hacer la cuenta concierto método ya que si no será fácil olvidar alguno o contar uno mas de una vez.
EDADES
Si se suma la edad de Pedro al cuadrado con la de Lucía la suma es 62 pero si se suma el cuadrado de la edad de Lucía con la edad de Pedro se obtiene 176. ¿Puedes dar las edades de Pedro y de Lucía?
PASTEL
Un pastel se va a repartir entre 14 personas; la primera toma la quinta parte del pastel, y la segunda toma una sexta parte de lo que dejó la primera. Las otras 12 personas restantes deciden repartirse lo que queda del pastel en partes iguales. ¿Qué fracción de pastel le tocará a cada una?
SUMA DE PRIMOS
Los números 4 y 8 se pueden escribir como suma de dos números primos(4 =2 +2, 8 =3 + 5).
¿Cuantos números mayores que 3 y menores que 31 no se pueden escribir como la suma de 2 números primos?
¿Cuantos números mayores que 3 y menores que 31 no se pueden escribir como la suma de 2 números primos?
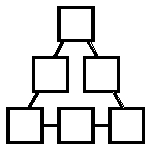
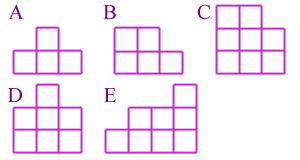
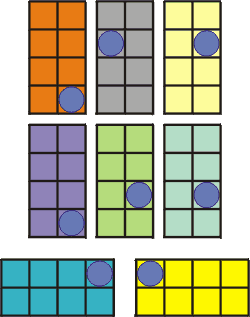
FIGURA
En la figura todos los lados largos son iguales y miden el doble de los cortos, que son todos iguales. Todos los ángulos son rectos y la figura tiene 200 cm2 de área. ¿Cuál es el perímetro?
CUADRO
Llena este cuadro con unos, doses, treses, cuatros o cincos de manera que cada cifra aparezca sólo una vez, en cada renglón, en cada columna y en cada una de las diagonales.
CARRERA
Armando corre más rápido que Beatriz, y Daniela siempre le gana a Cecilia en una carrera. A Beatriz y a Cecilia nunca les gana Eduardo. Un día hicieron una carrera entre todos. ¿En qué orden llegaron si Daniela llegó justo después de Armando y Beatriz le ganó a Cecilia?
CÍRCULOS
Si el círculo grande tiene radio r y los círculos pequeños tienen diámetro r, calcula la razón entre el área sombreada y el área del círculo grande.
ALTAS Y BAJAS
Cuando María se pone de pie sobre los hombros de Marcela puede ver justo por encima del muro. Cuando Marcela se pone de pie sobre los hombros de Mariana no ve mas que ladrillos. Cuando Mariana se pone de pie sobre los hombros de Margarita puede ver fácilmente por encima del muro. Si María se sube sobre los hombros de Mariana, María sólo ve ladrillos. ¿Quién es la más alta y quién es la más baja?
EL RELOJ Y EL ESPEJO
Al verse al espejo en la mañana, Sofía vio reflejado el reloj de manecillas en la pared y dijo: "El reloj se paró, marca las cuatro menos cinco". Sofía se equivocó. ¿Qué hora es en realidad?
FRUTAS
En una canasta hay manzanas, peras, naranjas y plátanos. Hay 44 frutas en la canasta. Hay 2 manzanas más que peras. Hay 8 peras más que plátanos. Hay dos plátanos más que naranjas. ¿Cuántas peras hay en la canasta?
PANECILLOS
La receta de ocho panecillos dulces tiene entre los ingredientes 20 grs. de mantequilla, 20grs. de azúcar y 40 grs. de harina. ¿Cuántos panes de éstos se pueden hacer si tenemos 140 grs. de mantequilla, 150 grs. de azúcar y 160 grs. de harina?
ESTATURAS
Pablo es 8 cm. más alto que Juan. Daniel es 12 cm. más bajo que Pablo y Juan mide 125 cm. ¿Cuánto mide Daniel?
PROBLEMA
Un auditorio tiene 25 filas y 25 butacas en cada una. Todas las butacas están numeradas empezando en la primera fila. ¿En qué fila se encuentra la butaca 458?
PROBLEMA
La cruz del dibujo está formada por 6 cuadrados. El perímetro es de 7 cm. ¿Cuál es el área de la cruz?
miércoles, junio 28, 2006
CRUZAR UN RÍO....DOS CLÁSICOS
Cruzar un río no supone un problema si se dispone, por ejemplo, de un puente.
Pero en determinadas circunstancias las cosas no son tan simples; veamos dos clásicos ejemplos de este tipo de problemas.
EL CAMPESINO
Un campesino realiza un viaje a pie con un lobo, un cordero y una col; en un punto de su travesía debe cruzar un río, para lo que dispone de un bote que sólo es capaz de transportar al campesino y a uno de sus tres tesoros. Por obvias razones el campesino no puede dejar a la oveja con el lobo, ni tampoco la oveja con la col. No tiene dónde ni con qué atar al lobo ni al cordero, ni tiene de donde colgar la col. Tampoco hay puentes. Nadie se mete al agua. ¿Cómo logra el campesino cruzar el río con sus animales y su col?
LOS MARIDOS CELOSOS
Tres maridos celosos y sus respectivas esposas tienen que cruzar el río en un bote que sólo puede llevar a dos personas en cada viaje. ¿Cómo logran cruzar todos ellos el río de forma que nunca una mujer queda en compañía de uno o dos hombres si su marido no esta presente?
No se aceptan como válidas, soluciones del tipo: "se arremangan los pantalones..." o "construyen un puente..." .
Pero en determinadas circunstancias las cosas no son tan simples; veamos dos clásicos ejemplos de este tipo de problemas.
EL CAMPESINO
Un campesino realiza un viaje a pie con un lobo, un cordero y una col; en un punto de su travesía debe cruzar un río, para lo que dispone de un bote que sólo es capaz de transportar al campesino y a uno de sus tres tesoros. Por obvias razones el campesino no puede dejar a la oveja con el lobo, ni tampoco la oveja con la col. No tiene dónde ni con qué atar al lobo ni al cordero, ni tiene de donde colgar la col. Tampoco hay puentes. Nadie se mete al agua. ¿Cómo logra el campesino cruzar el río con sus animales y su col?
LOS MARIDOS CELOSOS
Tres maridos celosos y sus respectivas esposas tienen que cruzar el río en un bote que sólo puede llevar a dos personas en cada viaje. ¿Cómo logran cruzar todos ellos el río de forma que nunca una mujer queda en compañía de uno o dos hombres si su marido no esta presente?
No se aceptan como válidas, soluciones del tipo: "se arremangan los pantalones..." o "construyen un puente..." .
SUMAS EXTRAÑAS
Observe las siguientes sumas, un tanto extrañas:
UNO + SIETE = OCHO
SEIS + CUATRO = DIEZ
CINCO + CINCO = DIEZ
DOS + NUEVE = OCHO
CUATRO + CINCO = ONCE
TRES + OCHO = ???
Las tres primeras parecen normales, pero las dos que siguen son mas bien raras.¿Serás capaz de completar la última?
UNO + SIETE = OCHO
SEIS + CUATRO = DIEZ
CINCO + CINCO = DIEZ
DOS + NUEVE = OCHO
CUATRO + CINCO = ONCE
TRES + OCHO = ???
Las tres primeras parecen normales, pero las dos que siguen son mas bien raras.¿Serás capaz de completar la última?
martes, junio 27, 2006
Bebés matemáticos
Antes de hablar o caminar los bebés ya entienden de números, afirma el estudio.
Antes de poder hablar o caminar los bebés ya tienen una noción rudimentaria de las matemáticas, asegura un estudio.
Para cuando cumplen 7 meses, los niños ya tienen una comprensión abstracta de los números.
Además, son capaces de correlacionar el número de voces que oyen con el número de caras que ven, afirman los científicos de la Universidad de Duke en Carolina del Norte, EE.UU., que llevaron a cabo la investigación.
Según expertos, las conclusiones del estudio podrían ser útiles a la hora de diseñar métodos para enseñar matemáticas a los más pequeños.
"¡Mira!"
Para llevar a cabo la investigación, Kerry Jordan y Elizabeth Brannon de la Universidad de Duke le mostraron a bebés de siete meses una grabación de dos o tres mujeres adultas desconocidas, que decían simultáneamente la palabra "look" ("mira").
Los videos fueron mostrados en dos pantallas puestas una al lado de la otra, que los bebés observaban desde los regazos de sus padres.
Una grabación de audio sincronizada con las imágenes de ambos videos podía escucharse desde una consola escondida.
En promedio, los niños pasaron una proporción significativamente más grande de su tiempo mirando la pantalla que mostraba el número de caras coincidente con el número de voces que oían.
"Nuestros resultados demuestran que para los siete meses de edad los niños pueden representar la equivalencia entre el número de voces que oyen y el número de caras que ven", afirmaron las autoras del estudio, publicado en el medio científico Proceedings of the National Academy of Sciences
Antes de poder hablar o caminar los bebés ya tienen una noción rudimentaria de las matemáticas, asegura un estudio.
Para cuando cumplen 7 meses, los niños ya tienen una comprensión abstracta de los números.
Además, son capaces de correlacionar el número de voces que oyen con el número de caras que ven, afirman los científicos de la Universidad de Duke en Carolina del Norte, EE.UU., que llevaron a cabo la investigación.
Según expertos, las conclusiones del estudio podrían ser útiles a la hora de diseñar métodos para enseñar matemáticas a los más pequeños.
"¡Mira!"
Para llevar a cabo la investigación, Kerry Jordan y Elizabeth Brannon de la Universidad de Duke le mostraron a bebés de siete meses una grabación de dos o tres mujeres adultas desconocidas, que decían simultáneamente la palabra "look" ("mira").
Los videos fueron mostrados en dos pantallas puestas una al lado de la otra, que los bebés observaban desde los regazos de sus padres.
Una grabación de audio sincronizada con las imágenes de ambos videos podía escucharse desde una consola escondida.
En promedio, los niños pasaron una proporción significativamente más grande de su tiempo mirando la pantalla que mostraba el número de caras coincidente con el número de voces que oían.
"Nuestros resultados demuestran que para los siete meses de edad los niños pueden representar la equivalencia entre el número de voces que oyen y el número de caras que ven", afirmaron las autoras del estudio, publicado en el medio científico Proceedings of the National Academy of Sciences
TRIÁNGULO
Es un polígono de tres lados, es decir, una porción de plano limitada por tres segmentos unidos, dos a dos, por sus extremos. Los tres segmentos que limitan el triángulo se denominan lados, y los extremos de los lados, vértices.
En un triángulo se consideran dos tipos de ángulos : interior (formado por dos lados) y exterior (formado por un lado y la prolongación de otro).
Consideraciones :
En todo triángulo, la suma de los ángulos interiores es igual a dos rectos.
En todo triángulo, un ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes.
Dos triángulos son iguales cuando tienen iguales un lado y sus dos ángulos adyacentes.
Dos triángulos son iguales cuando tienen dos lados iguales y el ángulo comprendidos.
Dos triángulos son iguales cuando tienen los tres lados iguales.
En todo triángulo, a mayor lado se opone mayor ángulo.
Si un triángulo tiene dos lados iguales, sus ángulos opuestos son también iguales.
En todo triángulo, un lado es menor que la suma de los otros dos y mayor que su diferencia.
C L A S I F I C A C I Ó N D E L O S T R I Á N G U L O S
Según sus lados
Equiláteros (sus tres lados iguales)
Isósceles (dos lados iguales y uno desigual)
Escaleno (tres lados desiguales)
Según sus ángulos
Rectángulos (un ángulo recto)
Acutángulos (tres ángulos agudos)
Obtusángulos (un ángulo obtuso)
En un triángulo se consideran dos tipos de ángulos : interior (formado por dos lados) y exterior (formado por un lado y la prolongación de otro).
Consideraciones :
En todo triángulo, la suma de los ángulos interiores es igual a dos rectos.
En todo triángulo, un ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes.
Dos triángulos son iguales cuando tienen iguales un lado y sus dos ángulos adyacentes.
Dos triángulos son iguales cuando tienen dos lados iguales y el ángulo comprendidos.
Dos triángulos son iguales cuando tienen los tres lados iguales.
En todo triángulo, a mayor lado se opone mayor ángulo.
Si un triángulo tiene dos lados iguales, sus ángulos opuestos son también iguales.
En todo triángulo, un lado es menor que la suma de los otros dos y mayor que su diferencia.
C L A S I F I C A C I Ó N D E L O S T R I Á N G U L O S
Según sus lados
Equiláteros (sus tres lados iguales)
Isósceles (dos lados iguales y uno desigual)
Escaleno (tres lados desiguales)
Según sus ángulos
Rectángulos (un ángulo recto)
Acutángulos (tres ángulos agudos)
Obtusángulos (un ángulo obtuso)
domingo, junio 25, 2006
VÍNCULOS PARA APRENDER DERIVADAS
http://soko.com.ar/matem/matematica/Derivada.htm
http://www.math2.org/math/derivatives/es-tableof.htm
http://www.fisicanet.com.ar/matematica/ma_3_derivadas.php
http://www.unlu.edu.ar/~mapco/apuntes/410/mapco410.htm
http://personal.redestb.es/javfuetub/analisis/calculo/derivada.htm
http://descartes.cnice.mec.es/Bach_CNST_1/Derivadas_aplicaciones_optimizacion/pag1.htm
http://webs.ono.com/usr011/siglo21/derivadas.htm
http://www.math2.org/math/derivatives/es-tableof.htm
http://www.fisicanet.com.ar/matematica/ma_3_derivadas.php
http://www.unlu.edu.ar/~mapco/apuntes/410/mapco410.htm
http://personal.redestb.es/javfuetub/analisis/calculo/derivada.htm
http://descartes.cnice.mec.es/Bach_CNST_1/Derivadas_aplicaciones_optimizacion/pag1.htm
http://webs.ono.com/usr011/siglo21/derivadas.htm
lunes, junio 12, 2006
LAS CINCO CIFRAS.......PROBLEMA
Se trata de encontrar cinco cifras consecutivas que cumplan la condición siguiente:
La suma de los cuadrados de las dos cifras más grandes debe de ser igual a la suma de los cuadrados de las otras tres cifras. ¿Que cifras son estas?
La suma de los cuadrados de las dos cifras más grandes debe de ser igual a la suma de los cuadrados de las otras tres cifras. ¿Que cifras son estas?
domingo, junio 11, 2006
CONSEJOS PARA RESOLVER SUDOKUS
Aquí van algunos de los primeros y más triviales consejos para principiantes:
*(1a) Utiliza lápiz y goma de borrar – Algunas veces te equivocarás y cuando eso suceda tendrás que «retroceder movimientos» o, normalmente, borrar el puzzle entero y empezar de nuevo. El bolígrafo no es buen amigo, aunque hay quien prefiere usar bolígrafo para marcar los números de los que está absolutamente seguro que están bien y lápiz para los «no tan seguros».
*(1b) Un Sudoku tiene una única solución - Teniendo esto en cuenta parece claro que cada número que descubras para cada casilla deberá ser uno y solamente uno entre todos los posibles. Cada paso puede deducirse por pura lógica, y todos esos pasos llevan a una única solución. Sólo debes marcar como buenos los números que sean los únicos posibles en cada casilla: si en alguna casilla pueden ir dos o tres números, examina las demás y vuelve a esa más adelante.
*(1c) Empieza por los números más frecuentes – Suele ser más fácil adivinar los números que faltan cuantos más números iguales de un mismo valor haya. Si lo piensas, cuando haya ocho números iguales repartidos por el tablero, la posición del noveno será casi trivial: la casilla intersección de la fila y columna en las que no está ese número.
*(1d) Empieza utilizando un método de eliminación - Puedes eliminar números de las casillas o casillas para un número. Por ejemplo, examina las casillas eliminando para ella los números del 1 al 9 que ya están en esa fila y columna y por tanto «no pueden ir ahí», hasta quedarte sólo con uno. Ese será el correcto. El otro sistema que usa mucha gente es eliminar las casillas de cada región, fijándose en las cifras que hay por toda la matriz y haciendo un «barrido» que «oscurece» o pone «cruces» a las casillas en donde no puede cierta cifra. Entonces, cuando hay un hueco libre en una sola casilla de una región, ahí es donde debe ir esa cifra.
*(1e) Al eliminar números, recuerda usar también las regiones cuadradas - No te fijes sólo en las filas y columnas que cruzan cada casilla. Tampoco puede haber en una casilla ningún número que ya esté repetido en el mismo cuadrado (región). De hecho, fijarse primero en las regiones suele ayudar a eliminar números más rápidamente incluso: un número «elimina» hasta tres posibles huecos en la misma región (de una fila o una columna).
*(1f) Escribe números «pequeñitos» para ayudarte – Hay gente que resuelve los Sodokus escribiendo los «números posibles» de cada casilla en pequeñito, en una esquina (y en grande en el centro los correctos). A medida que se pueden descartar esos «números pequeñitos», los van borrando. Cuando sólo queda uno, ese es el correcto. Esto a veces ayuda a descubrir números que habías pasado por alto o a ver otras pautas que ayudan a encontrar la solución.
*(1g) Empieza por los Sodokus de nivel muy fácil o fácil – Si empiezas por los difíciles o diabólicos puede resultar muy frustrante, y hacer los Sodokus tiene que ser divertido. Practica con los fáciles que ya aprenderás para los más complicados.
*(1h) Una vez que hayas terminado, haz un repaso rápido para comprobar que todo está bien – Haz una revisión contando números por orden en filas, columnas y regiones. A veces se cuela un pequeño error y el Sudoku parece resuelto pero en realidad está mal.
Eliminación por filas y columnas
La forma más sencilla de comenzar a resolver un Sudoku es el de eliminación. Se van eliminando casillas, o números, hasta quedarse con una única opción (número) para una casilla. Esa será la solución correcta para esa casilla, dado que el Sudoku sólo tiene una posible solución.
Eliminación por regiones
Además de eliminar números posibles por filas y columnas la eliminación de números por regiones es una técnica que resulta muy poderosa cuando por la situación de los números se puede utilizar.
Casillas en cruces de filas y columnas
Hay un método bastante básico pero efectivo para localizar algunos números rebeldes que no se descubren empleando los métodos de eliminación. A falta de una denominación estándar podría llamarse «casillas que hay en cruces de filas, columnas», o simplemente «cruces». Consiste en fijarse en una casilla que esté situada en un cruce de filas y columnas en las que haya muchos números y comprobarlos todos por orden, del 1 al 9, observando cuáles no pueden ser porque ya están en esas filas o columnas, para ver si con un poco de suerte sólo queda uno.
*(1a) Utiliza lápiz y goma de borrar – Algunas veces te equivocarás y cuando eso suceda tendrás que «retroceder movimientos» o, normalmente, borrar el puzzle entero y empezar de nuevo. El bolígrafo no es buen amigo, aunque hay quien prefiere usar bolígrafo para marcar los números de los que está absolutamente seguro que están bien y lápiz para los «no tan seguros».
*(1b) Un Sudoku tiene una única solución - Teniendo esto en cuenta parece claro que cada número que descubras para cada casilla deberá ser uno y solamente uno entre todos los posibles. Cada paso puede deducirse por pura lógica, y todos esos pasos llevan a una única solución. Sólo debes marcar como buenos los números que sean los únicos posibles en cada casilla: si en alguna casilla pueden ir dos o tres números, examina las demás y vuelve a esa más adelante.
*(1c) Empieza por los números más frecuentes – Suele ser más fácil adivinar los números que faltan cuantos más números iguales de un mismo valor haya. Si lo piensas, cuando haya ocho números iguales repartidos por el tablero, la posición del noveno será casi trivial: la casilla intersección de la fila y columna en las que no está ese número.
*(1d) Empieza utilizando un método de eliminación - Puedes eliminar números de las casillas o casillas para un número. Por ejemplo, examina las casillas eliminando para ella los números del 1 al 9 que ya están en esa fila y columna y por tanto «no pueden ir ahí», hasta quedarte sólo con uno. Ese será el correcto. El otro sistema que usa mucha gente es eliminar las casillas de cada región, fijándose en las cifras que hay por toda la matriz y haciendo un «barrido» que «oscurece» o pone «cruces» a las casillas en donde no puede cierta cifra. Entonces, cuando hay un hueco libre en una sola casilla de una región, ahí es donde debe ir esa cifra.
*(1e) Al eliminar números, recuerda usar también las regiones cuadradas - No te fijes sólo en las filas y columnas que cruzan cada casilla. Tampoco puede haber en una casilla ningún número que ya esté repetido en el mismo cuadrado (región). De hecho, fijarse primero en las regiones suele ayudar a eliminar números más rápidamente incluso: un número «elimina» hasta tres posibles huecos en la misma región (de una fila o una columna).
*(1f) Escribe números «pequeñitos» para ayudarte – Hay gente que resuelve los Sodokus escribiendo los «números posibles» de cada casilla en pequeñito, en una esquina (y en grande en el centro los correctos). A medida que se pueden descartar esos «números pequeñitos», los van borrando. Cuando sólo queda uno, ese es el correcto. Esto a veces ayuda a descubrir números que habías pasado por alto o a ver otras pautas que ayudan a encontrar la solución.
*(1g) Empieza por los Sodokus de nivel muy fácil o fácil – Si empiezas por los difíciles o diabólicos puede resultar muy frustrante, y hacer los Sodokus tiene que ser divertido. Practica con los fáciles que ya aprenderás para los más complicados.
*(1h) Una vez que hayas terminado, haz un repaso rápido para comprobar que todo está bien – Haz una revisión contando números por orden en filas, columnas y regiones. A veces se cuela un pequeño error y el Sudoku parece resuelto pero en realidad está mal.
Eliminación por filas y columnas
La forma más sencilla de comenzar a resolver un Sudoku es el de eliminación. Se van eliminando casillas, o números, hasta quedarse con una única opción (número) para una casilla. Esa será la solución correcta para esa casilla, dado que el Sudoku sólo tiene una posible solución.
Eliminación por regiones
Además de eliminar números posibles por filas y columnas la eliminación de números por regiones es una técnica que resulta muy poderosa cuando por la situación de los números se puede utilizar.
Casillas en cruces de filas y columnas
Hay un método bastante básico pero efectivo para localizar algunos números rebeldes que no se descubren empleando los métodos de eliminación. A falta de una denominación estándar podría llamarse «casillas que hay en cruces de filas, columnas», o simplemente «cruces». Consiste en fijarse en una casilla que esté situada en un cruce de filas y columnas en las que haya muchos números y comprobarlos todos por orden, del 1 al 9, observando cuáles no pueden ser porque ya están en esas filas o columnas, para ver si con un poco de suerte sólo queda uno.
jueves, mayo 25, 2006
NOTA DEL AUTOR
ESTE BLOG ESTÁ SIENDO REALIZADO POR ERNESTO DÍAZ.
VIVO EN SANTANDER Y MIS AFICIONES SON LAS MATEMÁTICAS ,COMO VEIS, EL AJEDREZ
,LOS VIAJES, INTERNET Y.....MÁS COSAS.
SI QUERÉIS MANDARME ALGÚN COMENTARIO :
EDIDIAZ11@HOTMAIL.COM
EDIDIAZ12@HOTMAIL.COM
EDIDIAZ@COLEGIOKOSTKA.COM
GRACIAS
VIVO EN SANTANDER Y MIS AFICIONES SON LAS MATEMÁTICAS ,COMO VEIS, EL AJEDREZ
,LOS VIAJES, INTERNET Y.....MÁS COSAS.
SI QUERÉIS MANDARME ALGÚN COMENTARIO :
EDIDIAZ11@HOTMAIL.COM
EDIDIAZ12@HOTMAIL.COM
EDIDIAZ@COLEGIOKOSTKA.COM
GRACIAS
LOS AZULEJOS EN EL INSTITUTO
Este modelo está formado por azulejos blancos y negros. Su anchura es de 7 azulejos. En el patio de un instituto hay uno como éste con una anchura de 149 azulejos. ¿Cuántos azulejos tendrá en total?.
PUZZLE
Ubique todas las piezas en un tablero de 8x8 de modo de que no haya dos círculos en la misma hilera, columna o en diagonal. Como ejemplo, la figura de la derecha muestra situaciones incorrectas, pues los círculos se encuentran en la misma diagonal.
TRIANGULO MÁGICO
Coloca los números del 1 al 9, de forma que la suma de los números de cada lado sea 20.
TRES AROS MÁGICOS
Coloca los números del 1 al 6, de forma que cada aro sume lo mismo. Hay 3 aros, cada uno engarza 4 círculos.
TRES EN RAYA MÁGICO
Coloca sobre la figura los números del 1 al 7, de forma que la suma de cada línea de las indicadas sea 12.
CRUZ MÁGICA
Coloca los números del 1 al 9, de forma que la línea horizontal, la vertical y las demás líneas indicadas, sumen lo mismo.
PUZZLE DE LA CRUZ
Ubique las piezas de la figura de modo de formar una cruz. Las piezas pueden rotarse.
ACERTIJOS CON HISTORIA
Un poco de historia: Sabemos que la gran pasión de Euclides (nacido en Grecia, alrededor del año 330 a. C.) era la geometría; su mayor contribución a la matemática fueron los trece libros que conforman Los elementos: los libros I a VI se concentran en la en la geometría plana (de dos dimensiones) y los libros XI a XIII, tratan de la geometría sólida (de tres dimensiones). Los elementos conforman un cuerpo de conocimientos tan completo que su contenido sería el currículo de geometría en colegios y universidades durante los siguientes dos mil años.
El matemático que compiló el texto equivalente, Arithmetica, para la teoría de números, fue Diofanto de Alejandría, el último exponente de la tradición matemática griega. De él se desconoce su lugar y época de nacimiento. Su llegada a Alejandría pudo haber ocurrido en cualquier momento dentro de un lapso de cinco siglos. El único dato acerca de la vida de Diofanto que ha sobrevivido aparece en forma de un acertijo que, se dice, estaba inscripto en su tumba:
" Aquí fueron sepultados los restos de Diofanto. La infancia de Diofanto duró 1/6 de su vida, 1/12 en la adolescencia, cuando la barba cubrió su cara, Después de 1/7 de su vida contrajo nupcias. Luego de cinco años de casado nació su primer hijo. El hijo vivió ½ de la vida de su padre, su padre buscó consuelo en los números pero no lo logró y murió cuatro años después que él."
Tratemos de averiguar cuantos años vivió Diofanto.
El matemático que compiló el texto equivalente, Arithmetica, para la teoría de números, fue Diofanto de Alejandría, el último exponente de la tradición matemática griega. De él se desconoce su lugar y época de nacimiento. Su llegada a Alejandría pudo haber ocurrido en cualquier momento dentro de un lapso de cinco siglos. El único dato acerca de la vida de Diofanto que ha sobrevivido aparece en forma de un acertijo que, se dice, estaba inscripto en su tumba:
" Aquí fueron sepultados los restos de Diofanto. La infancia de Diofanto duró 1/6 de su vida, 1/12 en la adolescencia, cuando la barba cubrió su cara, Después de 1/7 de su vida contrajo nupcias. Luego de cinco años de casado nació su primer hijo. El hijo vivió ½ de la vida de su padre, su padre buscó consuelo en los números pero no lo logró y murió cuatro años después que él."
Tratemos de averiguar cuantos años vivió Diofanto.
domingo, mayo 14, 2006
ROMPECABEZAS GEOMÉTRICO
Acomode las fichas como muestra la figura de modo de que los colores de fichas adyacentes coincidan. Las piezas pueden rotarse.
Ecuaciones con Palabras
Este tipo de pasatiempo apareció por primera vez en la revista Games, en mayo-junio de 1981. Will Shortz propuso en esa ocasión 24 "ecuaciones", y debido al éxito que tuvieron la revista siguió publicando este tipo de "ecuaciones" en números posteriores.El objetivo es reemplazar las letras por palabras de modo de que quede una frase 'correcta'.
Ejemplos:
7 = D en una S => 7 días en una semana
50 = E en E U => 50 Estados en Estados Unidos
12 = D de J
Ejemplos:
7 = D en una S => 7 días en una semana
50 = E en E U => 50 Estados en Estados Unidos
12 = D de J
BUSCA LA SOLUCIÓN EN :
miércoles, mayo 10, 2006
LA CENA
Carlos, Manolo, Federico y Luis fueron a cenar en compañia de sus esposas. En la cena se sentaron alrededor de una mesa redonda de forma que:
- ningún marido quedó al lado de su esposa
- enfrente de Carlos se sentó Federico
- a la derecha de la esposa de Carlos se sentó Manolo
- no había dos hombres juntos
¿Quién se sentó entre Carlos y Luis?
sábado, mayo 06, 2006
DICCIONARIO
Abscisa
Medida tomada sobre el eje horizontal en el sistema de coordenadas cartesiano.Es el primero de las dos coordenadas que hacen referencia a un punto.Así, el punto de coordenadas (3, 2) tiene como abscisa el número 3.
Medida tomada sobre el eje horizontal en el sistema de coordenadas cartesiano.Es el primero de las dos coordenadas que hacen referencia a un punto.Así, el punto de coordenadas (3, 2) tiene como abscisa el número 3.
ILUSIÓN
Intenta decir el color de las palabras. No leer la palabra, sino decir el color en que están escritas.
Cuesta, ¿verdad? Eso es debido a que tu parte derecha del cerebro quiere decir el color, pero tu parte izquierda insiste en leer la palabra.
DICCIONARIO
Ábaco
Tablero para realizar operaciones aritméticas trasladando manualmente una serie de fichas a lo largo de unas varillas.Se ha utilizado hasta épocas muy recientes en China y Japón y puede considerarse como la primera de las calculadoras
ILUSION
Mira fijamente el puntito del centro del dibujo... ahora aleja y acerca tu cabeza rápidamente y sin perder de vista el punto... ¡Los elementos que lo rodean giran entre sí a la velocidad de tu cabeza!
DICCIONARIO
Arista
1.- Lado de la cara de un poliedro
2.- Recta común de las caras de un diedro
3.- Arista de un haz: recta por la que pasan todos los planos de un haz de planos
1.- Lado de la cara de un poliedro
2.- Recta común de las caras de un diedro
3.- Arista de un haz: recta por la que pasan todos los planos de un haz de planos
viernes, mayo 05, 2006
HACE AÑOS....
Hace unos cuantos años recuerdo un día de octubre en que a medianoche llovía a cántaros en Santiago de Compostela. ¿Es posible que 72 horas más tarde el tiempo fuera allí soleado?
LIBROS
Alberto tiene al menos mil libros —dice Bárbara.
—No es cierto —dice Carlos—, tiene menos.
—Pues seguro que tiene al menos uno —interviene Delia.
Si sólo una afirmación es cierta, ¿cuántos libros tiene Alberto?
—No es cierto —dice Carlos—, tiene menos.
—Pues seguro que tiene al menos uno —interviene Delia.
Si sólo una afirmación es cierta, ¿cuántos libros tiene Alberto?
PROBLEMA DEL CAFÉ Y LA LECHE
Problema del café y la leche: Tenemos dos vasos iguales, uno con café, el otro con leche. Ambos contienen la misma cantidad de uno y otra.
Tomamos una cucharada del vaso de café, y la vertemos en el de leche. Mezclamos bien y seguidamente tomamos una cucharada del vaso de leche (que contendrá algo de café) y la vertemos en el de café.
Tras estas operaciones, el vaso de leche contiene un poco de café, y el de café contiene un poco de leche. ¿Qué hay más: café en la leche o leche en el café? ¿O igual?
Tomamos una cucharada del vaso de café, y la vertemos en el de leche. Mezclamos bien y seguidamente tomamos una cucharada del vaso de leche (que contendrá algo de café) y la vertemos en el de café.
Tras estas operaciones, el vaso de leche contiene un poco de café, y el de café contiene un poco de leche. ¿Qué hay más: café en la leche o leche en el café? ¿O igual?
Pitágoras de Samos
Nació : alrededor del 580 AC en Samos, Ionia
Falleció : alrededor del 500 AC en Metapontum, Lucania
Era originario de la isla de Samos, situado en el Mar Egeo. En la época de este filósofo la isla era gobernada por el tirano Polícrates. Como el espíritu libre de Pitágoras no podía avenirse a esta forma de gobierno, emigró hacia el occidente, fundando en Crotona (al sur de Italia) una asociación que no tenía el carácter de una escuela filosófica sino el de una comunidad religiosa. Por este motivo, puede decirse que las ciencias matemáticas han nacido en el mundo griego de una corporación de carácter religioso y moral. Ellos se reunían para efectuar ciertas ceremonias, para ayudarse mutuamente, y aun para vivir en comunidad. En la Escuela Pitagórica podía ingresar cualquier persona, ¡hasta mujeres!. En ese entonces, y durante mucho tiempo y en muchos pueblos, las mujeres no eran admitidas en la escuelas. Se dice que Pitágoras se casó con una de las alumnas. El símbolo de la Escuela de Pitágoras y por medio del cual se reconocían entre sí, era el pentágono estrellado, que ellos llamaban pentalfa (cinco alfas). Debido a la influencia política que tuvo la Escuela en esa época, influencia que era contraria a las ideas democráticas existentes, se produjo, tal vez, después del año 500 una revuelta contra ellos, siendo maltratados e incendiadas sus casas. Pitágoras se vio obligado a huir a Tarento, situada al sur de Italia. Algunos piensan que un año más tarde murió asesinado en otra revuelta popular en Metaponto. Se debe a Pitágoras el carácter esencialmente deductivo de la Geometría y el encadenamiento lógico de sus proposiciones, cualidades que conservan hasta nuestros días. La base de su filosofía fue la ciencia de los números, y es así como llegó a atribuirles propiedades físicas a las cantidades y magnitudes. Es así como el número cinco era el símbolo de color; la pirámide, el del fuego; un sólido simbolizaba la tetrada, es decir, los cuatro elementos esenciales: tierra, aire, agua y fuego.
Suscribirse a:
Entradas (Atom)